Projects:MultimodalAtlas
Back to NA-MIC_Collaborations, MIT Algorithms
In many medical image analysis applications we have a large collection of data sets available to us. In such applications, we are faced with at least two different challenges: first, most analyses we are interested in carrying out on the data-sets require point-wise spatial correspondence across the images. Co-registration of the image data set directly or indirectly attempts to solve this problem by spatially warping the images into a common, so-called “atlas space.” Another important challenge we face is coming up with a summary of the collection – this summary is usually called a template or an atlas, which is usually an average image. The famous MNI template brain, commonly used in neuroimaging studies is one example. Templates can be used to “normalize” new images, that is bring them into the common atlas space: for localizing regions of interests in the new subject or comparing groups of interest.
Recent work has acknowledged the fact that in some cases a single template may not suffice to summarize the whole population. For example, in Blezek and Miller MICCAI '06, the authors propose an atlas stratification algorithm that computes multiple templates. In this work, we propose and investigate an algorithm that jointly co-registers a collection of images while computing multiple templates. The algorithm, called iCluster for Image Clustering, is based on the following idea: given the templates, the co-registration problem becomes simple, reducing to a number of pairwise registration instances. On the other hand, if we are given a collection of images that have been co-registered, i.e. in perfect alignment, then an off-the shelf clustering or averaging algorithm can be used to compute the templates.
Description
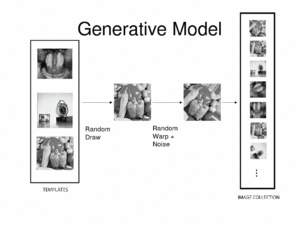
iCluster is derived from a simple generative model. We assume that there are a fixed and known number of template images. Then the process that generates an observed image is as follows: a template is randomly drawn – note that the probability that governs this process doesn’t have to be uniform. Next, the chosen template is warped with a random transformation and i.i.d Gaussian noise is added to this warped image to generate an observed image. This process is repeated multiple times to generate a collection of images.
We formulate the problem as a maximum likelihood solution. We employ a Generalized Maximum Likelihood algorithm to solve the problem.
In the E-step, the algorithm computes membership probabilities.
We divide the M-step into two sub-steps: the first one, called the T (template) step is where we have closed-form expressions for the optimization. The algorithm updates the template images as weighted averages of the images, where the weights are the memberships. The template priors are updated as normalized sums of memberships.
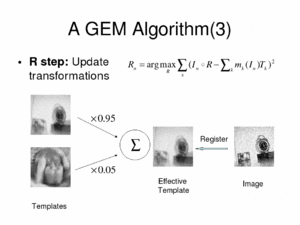
In the second part of the M-step, called R (registration) step, the algorithm performs a collection of independent pairwise registration instances. Each image is registered with a unique, "effective" template, which is a weighted average of the current templates and the weights are the corresponding memberships.