Projects:DTIFiberRegistration
Back to NA-MIC Collaborations, MIT Algorithms
Joint Registration and Segmentation of DWI Fiber Tractography
The purpose of this work is to jointly register and cluster DWI fiber tracts obtained from a group of subjects. We formulate a maximum likelihood problem which the proposed method solves using a generalized Expectation Maximization (EM) framework. Additionally, the algorithm employs an outlier rejection and denoising strategy to produce sharp probabilistic maps (an atlas) of certain bundles of interest. This atlas is potentially useful for making diffusion measurements in a common coordinate system to identify pathology related changes or developmental trends.
Description
Initial Registration
A spatial normalization is necessary to obtain a group-wise clustering of the resulting fibers. This initial normalization is performed on the Fractional Anisotropy (FA) images generated for each subject. This initial normalization aims to remove gross differences across subjects due to global head size and orientation. It is thus limited to a 9 parameter affine transformation that accounts for scaling, rotation and translation. The resulting transformations are then applied to each of the computed fibers to map them into a common coordinate frame for clustering.
Initial Fiber Clustering
Organization of tract fibers into bundles, in the entire white matter, reveals anatomical connections such as the corpus callosum and corona radiata. By clustering fibers from multiple subjects into bundles, these common white matter structures can be discovered in an automatic way, and the bundle models can be saved with expert anatomical labels to form an atlas. In this work, we take advantage of automatically segmented tractography that has been labeled (as bundles) with such an atlas for initialization.
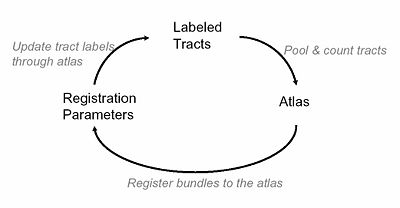
Joint Registration and Segmentation
Once we obtain an initial affine registration and clustering results using the high dimensional atlas, we iteratively fine-tune the registration and clustering results using a maximum likelihood framework, which is solved through a generalized EM algorithm. For the registration we use one set of affine parameters per fiber bundle, and combine these affine registrations into a single smooth and invertable warp field using a log-Euclidian poly-affine framework. Additionally, the algorithm employs an outlier rejection and denoising strategy while producing sharp probabilistic maps of certain bundles of interest.
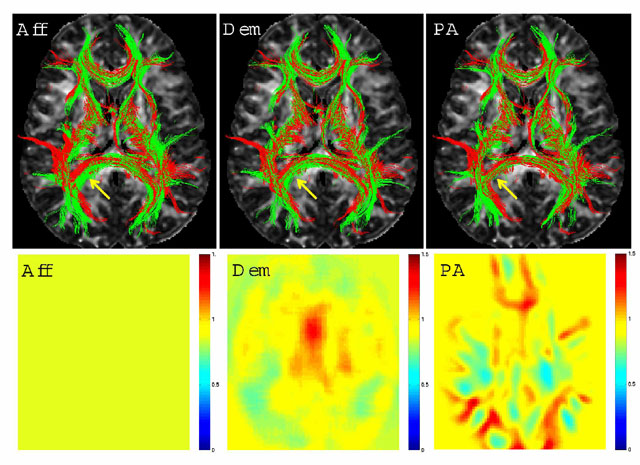
We tested the registration component of this algorithm without updating the clustering with 26 major fiber bundles. The poly-affine warp fields with relatively limited number of components resulted in similar quality registrations when compared with results from a benchmark non-linear registration algorithm that was run on FA images:
 Top Row: 3D renderings of the registered tracts of a subject (in green) and the template (in red) within 5mm of the central axial slice overlayed on the central FA slice of the template. Aff (left) stands for the FA based global affine, Dem (middle) for the demons algorithm and PA (right) for the proposed framework in this work. Arrows point to an area of differing qualities of registration. Overlapping of the red and green fibers is indicative of better registration. Bottom Row: Jacobian determinant images from the central slice of the volume: Yellow represents areas with small changes in size, and the shades of red and blue represent enlargement and shrinking, respectively. The Jacobian of the global affine registration is constant. The Jacobian of the demons algorithm is smooth due to the Gaussian regularization. The Jacobian of the new algorithm reflects the underlying anatomy because of the fiber bundle-based definition of the deformation. |
Corpus Callosum, Cingulum and the Fornix were selected for further investigation because of the specific challenges they present. These three structures are in close proximity with each other, and that results in many mislabeled fibers when labeled using a high dimensional atlas (see figure below (left)). Their close proximity also results in a number of trajectories deviating from one structure to another. These are precisely the sorts of artifacts we wish to reduce through learning common spatial distributions of fiber bundles from a group of subjects.
 Tracts from Fornix (in green) and Cingulum (in purple) bundles along with a few selected tracts from Corpus Callosum (in black) as labeled using the high dimensional atlas (left) and after the EM algorithm with tract cuts (right). The tractography noise is evident in the images on the left as tracts deviating from one bundle to another. Also, these images contain instances where the high dimensional atlas failed to label the tracts correctly. The EM algorithm is able to remove the segments of tract bundles that are not consistent from subject to subject. |
We also constructed two different atlases to compare the effects of labeling algorithms on the quality of resulting group maps. The first one is constructed using the initial labels from the high dimensional atlas. A second one is built using the proposed algorithm:
 Spatial distributions of Corpus Callosum, Cingulum and Fornix bundles from three single slices overlaid on their corresponding FA images. These maps are constructed using two different methods. a)High dimensional atlas, c) Proposed algorithm. The colorbars indicate the probability of each voxel in the spatial distribution of the corresponding fiber bundle. Note that the probabilities become higher in the central regions of the bundles and the number of sporadical voxels with non-zero probabilities decrease from left to right, indicating a sharper atlas through better registration and more consistent labeling of the subjects. |
Project Status
- Working 3D implementation in Matlab and C.
Key Investigators
- MIT Algorithms: Ulas Ziyan, Mert R. Sabuncu
- Harvard DBP1: Carl-Fredrik Westin, Lauren O'Donnell
