Projects:ShapeAnalysisWithOvercompleteWavelets
Back to NA-MIC Collaborations, MIT Algorithms
In this work, we extend the Euclidean wavelets to the sphere. The resulting over-complete spherical wavelets are invariant to the rotation of the spherical image parameterization. We apply the over-complete spherical wavelet to cortical folding development and show significantly consistent results as well as improved sensitivity compared with the previously used bi-orthogonal spherical wavelet. In particular, we are able to detect developmental asymmetry in the left and right hemispheres.
Description
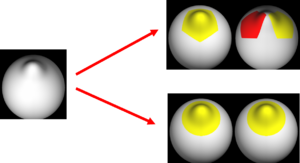
Bi-orthogonal spherical wavelets have been shown to be powerful tools in the segmentation and shape analysis of 2D closed surfaces [1,2], but unfortunately they suffer from aliasing problems and are therefore not invariant under rotations of the underlying surface parameterization. See the toy example in the figure below.
Instead, we propose to use the over-complete spherical wavelets. These over-complete spherical wavelets are based on filter bank theory, directly extending the ideas of Euclidean steerable pyramid to the sphere. We demonstrate the theoretical advantage of over-complete wavelets over bi-orthogonal wavelets. We also show that over-complete spherical wavelets allow us to build more stable cortical folding development models, and detect a wider array of regions of folding development in a newborn dataset. The use of spherical wavelet transform in cortical shape analysis allows us to study cortical folds of different spatial scales, which are difficult to analyze by cortical folding analysis methods based on local features such as curvature and sulcal depth measurements.
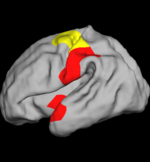
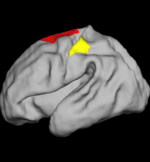
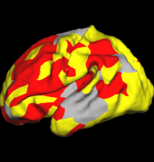
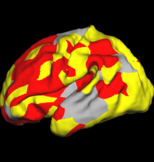
The two images on the left show the cortical folding speed detected by the bi-orthogonal wavelets. Notice, how the detection changes wildly with different parameterizations. On the other hand, the results of over-complete wavelets are stable across different parameterizations. Furthermore, the over-complete wavelets are much more sensitive than the bi-orthogonal wavelets in detecting changes.
[1] P. Yu, P. E. Grant, Y. Qi, X. Han, et al., "Cortical surface shape analysis based on spherical wavelets," IEEE Transaction on Medical Imaging, vol. 26, pp. 582-97, 2007.
[2] D. Nain, S. Haker, A. Bobick, and A. Tannenbaum, "Multiscale 3-d shape representation and segmentation using spherical wavelets," IEEE Transaction on Medical Imaging, vol. 26, pp. 598-618, 2007.
Key Investigators
- MIT Algorithms: [| B.T. Thomas Yeo], Peng Yu, Wanmei Ou, Ellent Grant, Bruce Fischl, Polina Golland
Publication
In Press
- B.T.T. Yeo, W. Ou, P. Golland. On the Construction of Invertible Filter Banks on the 2-Sphere. Yeo, Ou and Golland. Accepted to the IEEE Transactions on Image Processing [In Press]
- P. Yu, B.T.T. Yeo, P.E. Grant, B. Fischl, P. Golland. Cortical Folding Development Study based on Over-Complete Spherical Wavelets. In Proceedings of MMBIA: IEEE Computer Society Workshop on Mathematical Methods in Biomedical Image Analysis, 2007.
In Print