Engineering:TCON 05 05 2005

Agenda:

• Discussion of Programming Week infrastructure projects. (Steve, Mike)
• itk::SymmetricSecondRankTensor, itk::DiffusionTensor3D. (Luis)
• Dynamic loading of file formats in ITK (ITK IO Plugins). (Jim)
• ITK LabelStatisticsImageFilter (now with histograms), LabelMomentsImageFilter (under development). (Jim)

Attendees:

Rick Avila, Andy Cedilnik, Karthik Krishnan, Luis Ibanez, Tina Kapur, Jim Miller, Ron Kikinis, Steve Pieper, Michael Pan, Jagadeeswaran Rajendiran, Xiaodong tao

Meeting Notes:

SUN grid for Programmer's Week =

Steve has put in a request to SUN to provide a set of loaner machines (3 dual core, quad processor, 32GB RAM) for the upcoming programmer's week.

Slicer

Steve is looking at using the KW Widgets for the next version of slicer. These widgets provide a cross platform C++ abstraction for widgets in a VTK-like API. Currently the KW Widgets require the CVS version of VTK.

Tensor Images related code from Jeffrey Duda

• http://www.seas.upenn.edu/~jtduda/
• http://www.seas.upenn.edu/~jtduda/vector.html
• http://www.seas.upenn.edu/~jtduda/tensor.html

The new SymmetricSecondRankTensor class in ITK was largely based on Jeffrey's class, although his page points out that his class was also inspired from

http://www.na-mic.org/Wiki/index.php/NAMIC_Wiki:DTI:ITK-DiffusionTensorPixelType:Header

NRRD Header

Suggestions from discussions among Guido Gerig, Dave Tuch, Gordon Kindlmann and others NAMIC_Wiki:DTI:Tensor_format.

DTI in slicer

VTK class to estimate tensors: http://splweb.bwh.harvard.edu:8000/cgi-bin/develop/viewcvs.cgi/slicer2/Modules/vtkDTMRI/cxx/vtkImageDiffusionTensor.cxx?annotate=1.7&cvsroot=slicer

Code that uses slicer's vtkAG class to register tensor values: http://splweb.bwh.harvard.edu:8000/cgi-bin/develop/viewcvs.cgi/slicer2/Modules/vtkDTMRI/tcl/DTMRITensorRegistration.tcl?annotate=1.4&cvsroot=slicer

Xiaodong's ITK examples

Xiaodong has written some tensor reconstruction and analysis code using ITK. This code is currently in the sandbox http://www.na-mic.org:8000/websvn/listing.php?repname=NAMICSandBox&path=%2FNrrdDWITensorReconstruction%2F&rev=0&sc=0 This code needs to be packaged into the appropriate ITK filters and examples and use the new ITK tensor classes.

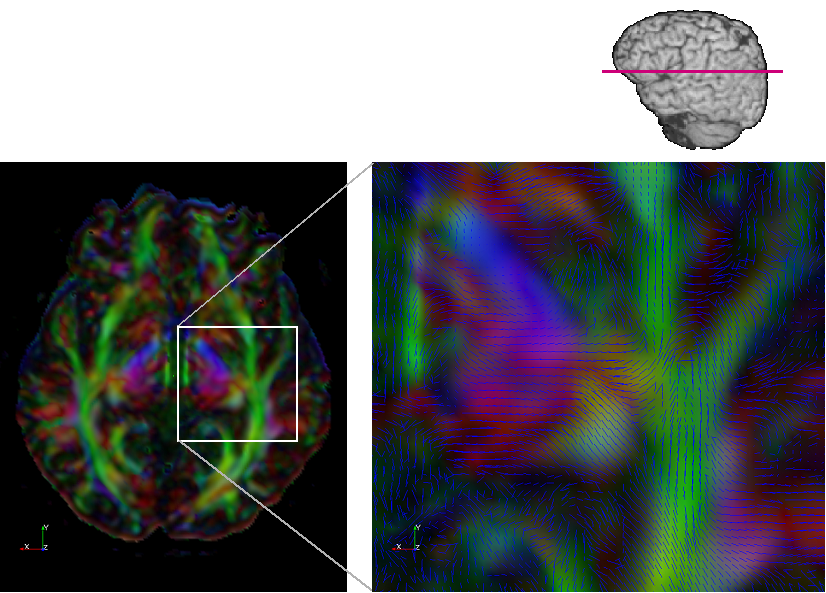
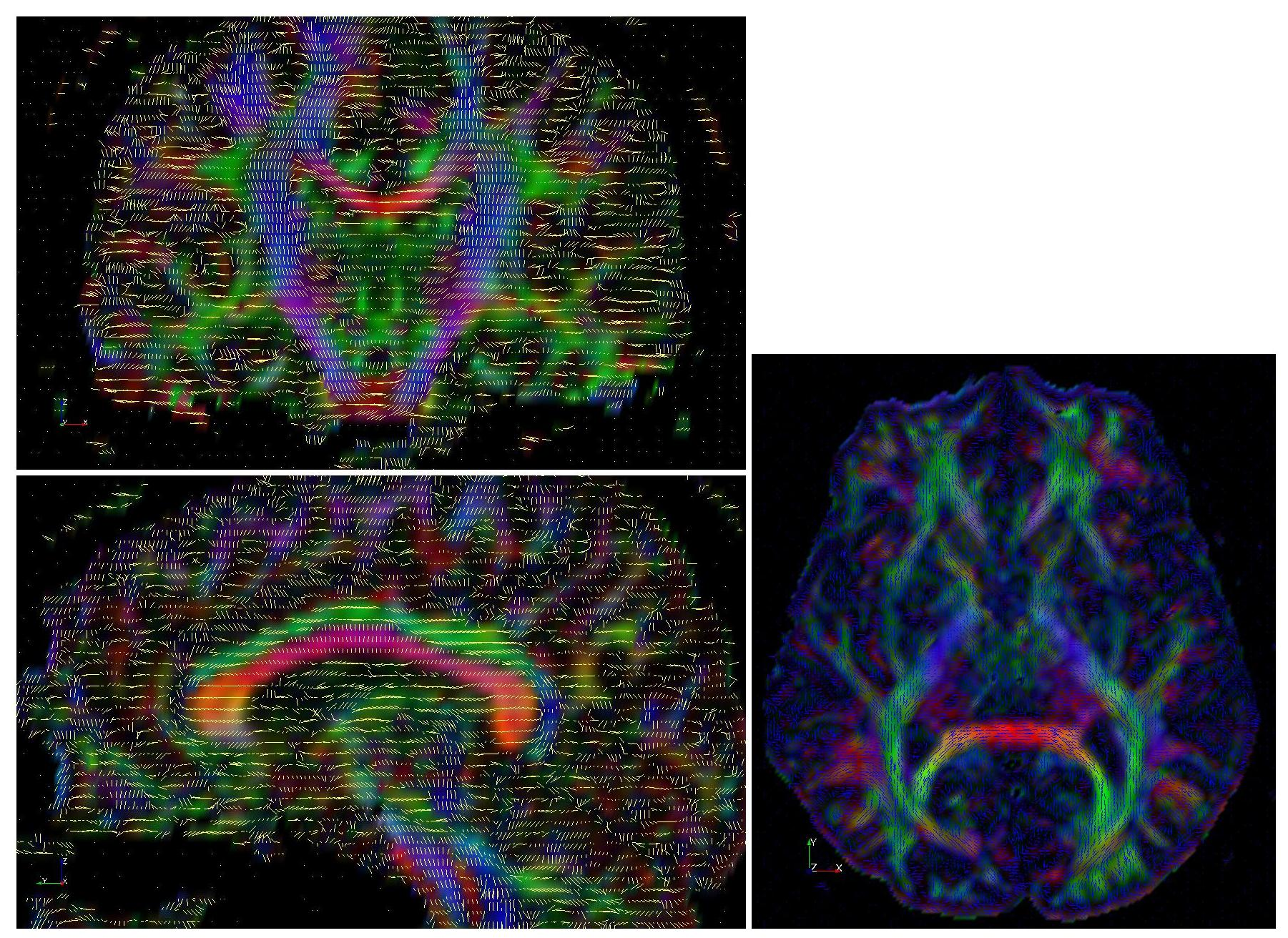
The following images show the fractional anisotropy colored by the components of the first principle direction, with red being x-component, green being y-component, and blue being z-component. The lines on the zoom-in view show the projections of the first principle direction (unit vectors) onto the plane. The line and the little brain on top shows the rough location of this axial slice.

 Correction: The vector field orientations in this image seem incorrect. Please check the orientations.
 

Fractional Anisotropy of an axial slice of a brain

The vectors shown above have wrong x-components. The reason was that the x component in the gradient directions is flipped. The following is an image showing the FA as well as the principal vectors computed using the CORRECTED gradient direction.

DTI example with corrected X gradient component

Tensor registration

With tensor support coming into ITK, the topic of tensor registration arose. For ITK to support tensor registration, we need to add an interpolator for tensor images and a metric from comparing two tensors. For comparing two tensors, Jim suggested using

t'r'a'c'e(A ^{- 1}B)

This is simple but not intuitively pleasing because for the scalar case, this becomes a/b instead of a-b which is normally used for comparing scalars. Paulo Mendonca at GE Research suggested using the Frobenius norm of A-B. This translates nicely back to the scalar metric. You can also justify the Frobenius norm if the desired metric is that the difference between the quadratic forms of two tensor be small everywhere

\int (x'Ax - x'Bx)^2 dx = \int (x'(A-B)x)^2 dx