Projects:NerveSegmentation

Back to NA-MIC Collaborations, MIT Algorithms,

Nerve Segmentation

Automatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task. In this paper, we present an automatic tracking method for nerve segmentation based on particle filters. We develop a novel approach to particle representation and dynamics, based on Bezier splines. Moreover, we introduce a robust image likelihood model that enables delineation of nerve bundles and ganglia from the surrounding anatomical structures. We demonstrate accurate and fast nerve tracking when compared to expert manual segmentation.

Data

We show three slices of an example High-Resolution MR scan. All arrows point to the same nerve bundle. Blue arrows show examples of poor contrast between the nerve and the surrounding tissue; orange arrows indicate the thickening of the neural tract into a ganglion.

Description

In this paper, we present a tracking approach based on particle filtering, also known as sequential Monte Carlo tracking. Tracking has also been used successfully for segmentation of tubular structures. Most vessel tracking methods model the state as a cross-sectional ellipse or as a cylindroid. In tracking nerve bundles, the regions of low contrast require the state to capture substantially longer segments of the track than what is represented by a cross-section. In addition, nerves tend to change direction, often sharply, which necessitates a use of more complex descriptors than cylinders.

To address the challenges of nerve tracking, we define a flexible particle representation that captures the geometric behavior of the nerve bundles. We use a Bezier spline centerline with a linear radius function to characterize a nerve bundle. We devise a dynamics model for particle updates that encourages continuity and smoothness. Furthermore, we define an image likelihood model that compares gradient fields and intensities of predicted patches with image observations to evaluate a posterior distribution of the particles' importance. Once tracking is completed, we remove spurious segmentations by measuring the quality of the entire tract. We demonstrate successful segmentations of neural tracts and evaluate them relative to expert manual segmentations. To the best of our knowledge, this is the first automatic segmentation of nerve bundles and ganglia.

Results

The above figure shows a summary of our results. On the left, we show a rendering of segmentation results -- the rightmost nerve shows results without post-processing pruning, while the left segmentation was processed after completion of tracking with an automatic post-processing step. On the right, we present two measures, precision and sensitivity, as box plots.

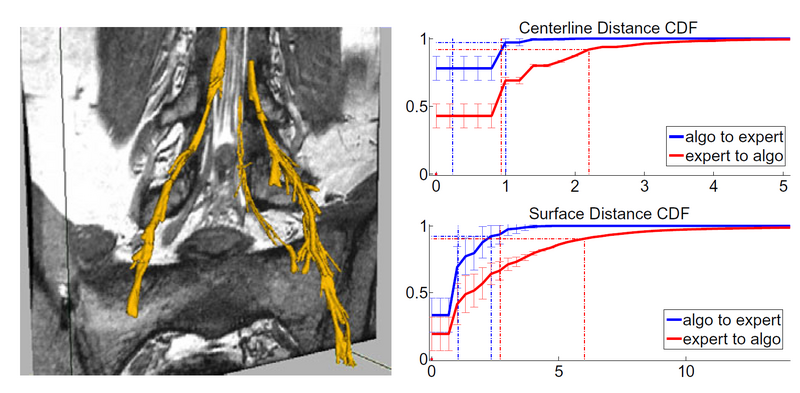
Here we compare our segmentations with expert delineations. We define precision as the percentage of voxels identified by the algorithm as nerve that were also marked as nerve by an expert. Precision coarsely quantifies our ability to separate the nerve from the surroundings. We also compute precision for a dilation of the manual segmentation by two and three voxels. The results for precision are shown in the left part of the graph, where we note that we reach a median~$97.3\%$ of our proposed segmentation being within 2 voxels of the expert segmentation, while due to partial volume effect we over-segment the thin nerves and we only achieve a 68% precision with respect to exact segmentation.

Since the main goal of nerve tracking is to extract the full path of the nerve accurately, while it is less crucial to identify the bundle boundaries, we also define sensitivity to quantify the agreement between the automatically defined path and the centerline of the manual segmentation. We define sensitivity as the percentage of voxels in the centerline of the expert segmentation that were also correctly identified by our algorithm. We also compute the same percentage for a dilation of the automatic segmentation, by two and three voxels. We achieve a media 96% of the centerline voxels being within 3 voxels of a prediction, while we find a drop to 53% when comparing with the exact centerline. The latter drop is due to segmentations in the areas of the thick ganglia, where our method under-segments, and may follow a slightly off-center path.

Conclusion

As shown in the results, the proposed segmentation may slightly over-segment (usually by at most two voxels) in thin areas and under-segment in thick areas, but will give a very good estimation of the nerve core and location.

Literature

Key Investigators

• MIT: Adrian Dalca, Polina Golland
• BWH: Giovanna Danagoulian, Ehud Schmidt