Projects:TractLongitudinalDTI

Back to Utah 2 Algorithms

Ongoing Work (Updated 10/02/2011)

Tract-based longitudinal modeling of DTI data

This project develops a methodology to explore subject-specific, DTI data obtained from brain's white matter tracts, available at multiple but often sparsely present timepoints. The challenge is to develop a continuous spatio-temporal growth model, given discrete 4D DWI images. This would enable comparison of growth trajectories across subjects and along tracts which are biologically of interest in developmental and pathological changes.

Background

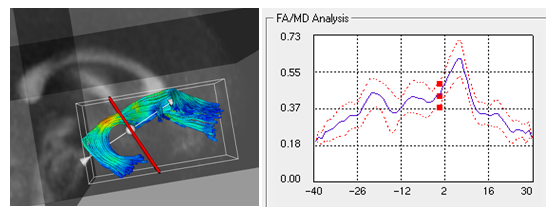
We use the arc length parametrization scheme initially proposed by Corouge et al. It represents white matter fiber tracts obtained via streamline tractography in the brain's atlas tensor image as a function of arc length. (Atlas construction uses unbiased atlas building schemes followed by back transformations to subjects' DTI images to obtain identical fiber tract geometry across subjects, populated with subject specific diffusion data). We use the mean diffusion scalar invariants derived from these individual fiber bundle cross sections, as our input longitudinal diffusion profiles.

White matter diffusion properties along fiber tract: Left: A fiber tract with an origin plane defined for arc length parametrization, Right: FA mean and standard deviation as function of arc-length. Dots mark location of coordinate origin.

Subject-specific spatiotemporal continuous growth model

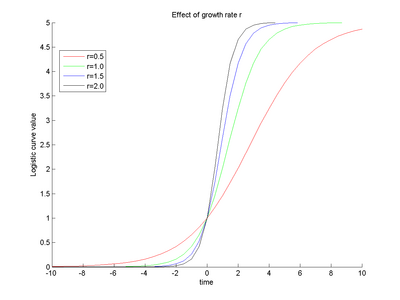
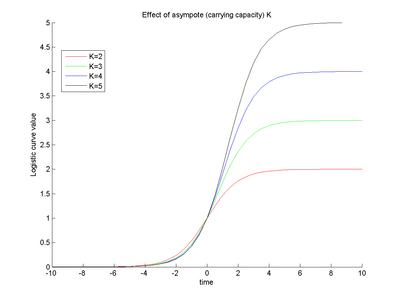
We propose the use of Verhulst-Pearl logistic equation to capture temporal changes, while using a non-parametric kernel along arc length to account for biologically motivated functional along-tract relationship in the diffusion data.

Logistic equation with P as the population value at a given time, r being the growth rate of the population and K being the carrying capacity (also the limiting asymptote value).

Effect of growth rate r on the logistic curve.

Effect of carrying capacity K on the logistic curve.

From the definition of the logistic function, the parameter r represents the growth rate of the diffusion invariant and the parameter K represents the asymptote value. The overall function shape intuitively follows the growth pattern we expect to see during brain maturation. The diffusion invariants start with an initial diffusion profile along tract, and have a non linear temporal growth trajectory showing maximum changes in early childhood and then slowing down or almost saturating at a certain age. (For instance, observed diffusion changes are much more in neonates than in an adult brain). The temporal trajectories may also differ along the tract's length giving localized changes. Since our method gives us continuous along-tract, growth trajectories all along time, we can compare subjects with respect to differences in diffusion profiles at birth, growth rates at any given age as well as the asymptote saturation values. This gives us important information to understand delayed or abnormal brain maturation by comparing a normative growth surface with an individual's or by comparing the model's parameters across subjects.

[[File:|600px|center|thumb|NOTES]]

References

[1] Corouge, I., Fletcher, P.T., Joshi, S., Gouttard, S., Gerig, G., 2006. Fiber tract-oriented statistics for quantitative diffusion tensor MRI analysis. Med Image Anal, pp. 786-798.

[2] Goodlett, C.B., Fletcher, P.T., Gilmore, J.H., Gerig, G., 2009. Group analysis of DTI fiber tract statistics with application to neurodevelopment. Neuroimage, pp. S133-142.

Key Investigators

• Utah: Anuja Sharma, Stanley Durrleman, Guido Gerig

Back to Utah 2 Algorithm Core