Projects:DTIFiberRegistration
Description
Collaborators: Ulas Ziyan (MIT), Mert Sabuncu (MIT), Lauren O'Donnell (BWH), Carl-Fredrik Westin (BWH)
Image registration is necessary to compare and combine information from a group of subjects. Affine registration (e.g. Talairach normalization) is common for group analysis, but this typically yields poor alignment accuracy in certain local regions of interest.
To address this, there has been interest in developing nonlinear registration methods. In nonlinear registration, the description and regularization of the deformation is critical, since an unconstrained registration algorithm suffers form the potential problem of overfitting to the images, which may undermine consecutive analyses. A popular approach is to employ a model-based regularization which may have no biological meaning. Yet, we believe that the regularization and description of the deformation should be grounded in the application.
In this project, we explore the use of anatomical structures (called fiber bundles) extracted from Diffusion MR Images of a group of subjects for regularizing a non-linear registration algorithm.
Segmentation
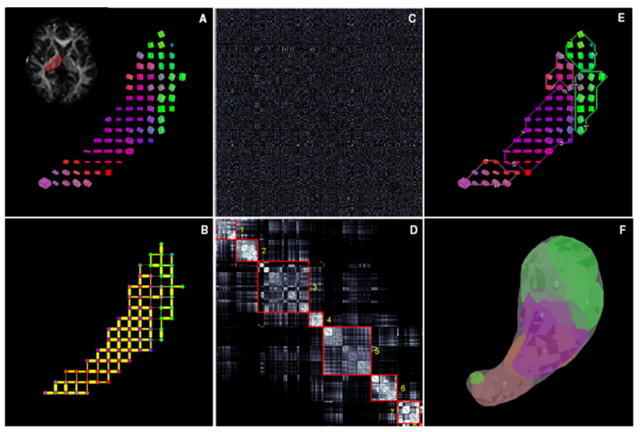
We are using a modified spectral clustering algorithm to segment the thalamic data.
This image is a schematic outline of spectral segmentation algorithm. (A) DTI data from an individual thalamic hemisphere, shown here as a single slice cuboid map (B) Initial graph corresponding to the sparse affinity matrix (C) Unordered affinity matrix (D) Ordered and clustered affinity matrix (E) Clusters in the original data space (F) Clusters in 3D.
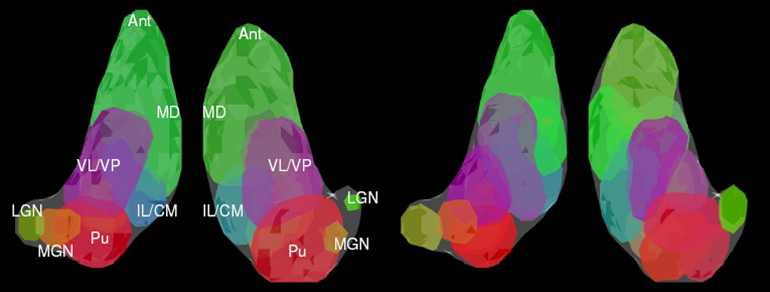
On the left there is a 3D rendering of expert segmentation of both hemispheres from one subject. On the right, it is the same subject segmented by the modified spectral clustering algorithm with 12 clusters. Clusters are colored according to their mean tensor orientations, therefore similar colors indicate similar mean tensor orientation.
Publications
Submitted for publication.
Software
The algorithms now are implemented in matlab.