Projects:DTIFiberRegistration

Description

Collaborators: Ulas Ziyan (MIT), Mert Sabuncu (MIT), Lauren O'Donnell (BWH), Carl-Fredrik Westin (BWH)

Image registration is necessary to compare and combine information from a group of subjects. Affine registration (e.g. Talairach normalization) is common for group analysis, but this typically yields poor alignment accuracy in certain local regions of interest.

To address this, there has been interest in developing nonlinear registration methods. In nonlinear registration, the description and regularization of the deformation is critical, since an unconstrained registration algorithm suffers form the potential problem of overfitting to the images, which may undermine consecutive analyses. A popular approach is to employ a model-based regularization which may have no biological meaning. Yet, we believe that the regularization and description of the deformation should be grounded in the application.

In this project, we explore the use of anatomical structures (called fiber bundles) extracted from Diffusion MR Images of a group of subjects for regularizing a non-linear registration algorithm.

Segmentation

Organization of tract fibers into bundles, in the entire white matter, reveals anatomical connections such as the corpus callosum and corona radiata. By clustering fibers from multiple subjects into bundles, these common white matter structures can be discovered in an automatic way, and the bundle models can be saved with expert anatomical labels to form an atlas. In this work, we take advantage of automatically segmented tractography that has been labeled (as bundles) with such an atlas.

Registration of Fiber Bundles

To align the bundles from two subjects, we compute 3 dimensional spatial probability maps for each fiber tract bundle in each subject. The goal of our registration is to maximize the correlation between two corresponding bundles' probability maps. To achieve that, we employ a sequential quadratic programming method to find the 9 affine parameters that maximize the correlation between corresponding probability maps in different subjects. For a pair of subjects, this yields a set of affine transformations that relate each corresponding bundle pair. The last step of our algorithm is to fuse these affine transformations to achieve a global, invertible non-linear deformation. There are several ways to achieve this. In this study, we employed the log-Eucledian poly-affine framework which guarantees invertibility.

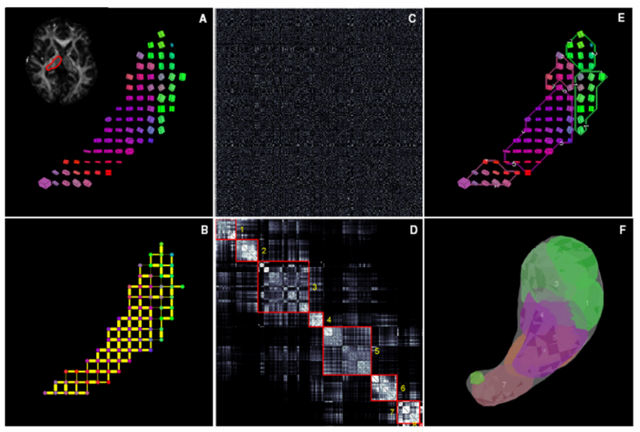
This image is a schematic outline of spectral segmentation algorithm. (A) DTI data from an individual thalamic hemisphere, shown here as a single slice cuboid map (B) Initial graph corresponding to the sparse affinity matrix (C) Unordered affinity matrix (D) Ordered and clustered affinity matrix (E) Clusters in the original data space (F) Clusters in 3D.

Publications

Submitted for publication.

Software

The algorithms now are implemented in matlab.