Difference between revisions of "Projects:DTIPopulationAnalysis"
| Line 74: | Line 74: | ||
''In Print'' | ''In Print'' | ||
| − | * [http://www.na-mic.org/publications/pages/display?search=DTIPopulationAnalysis&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database] | + | * [http://www.na-mic.org/publications/pages/display?search=DTIPopulationAnalysis&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Group Analysis of DTI Fiber Tracts] |
[[Category: Registration]] [[Category:Diffusion MRI]] [[Category:Schizophrenia]] | [[Category: Registration]] [[Category:Diffusion MRI]] [[Category:Schizophrenia]] | ||
Latest revision as of 20:29, 11 May 2010
Home < Projects:DTIPopulationAnalysisBack to NA-MIC Collaborations, Utah2 Algorithms, MIT Algorithms, UNC Algorithms
DTI ATlas Building
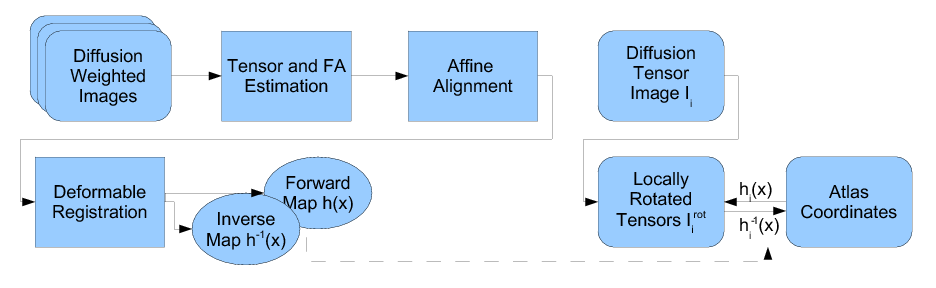
Our methodology for population analysis of DT-MRI is based on unbiased non-rigid registration of a population to a common coordinate system. The registration jointly produces an average DTI atlas, which is unbiased with respect to the choice of a template image, along with diffeomorphic correspondence between each image. The registration image match metric uses a feature detector for thin fiber structures of white matter, and interpolation and averaging of diffusion tensors use the Riemannian symmetric space framework. The anatomically significant correspondence provides a basis for comparison of tensor features and fiber tract geometry in clinical studies.
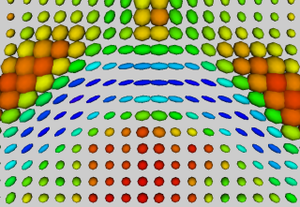
Our registration procedure is based on a scalar feature image which is sensitive to sheet like structures. We have observed that the major fiber bundles of interest occur as sheet or tube like manifolds in the FA image of the brain. As a feature image we use the maximum eigenvalue of the hessian of the FA image. Images are initially aligned using an affine registration and then deformed to a common coordinate system using the unbiased atlas-building procedure of Joshi et al. [1]. The deformation fields produced by the registration process are applied to the tensors fields using appropriate methods for reorienting and interpolating tensors. The transformed images are averaged in the atlas space to produce a DTI atlas.
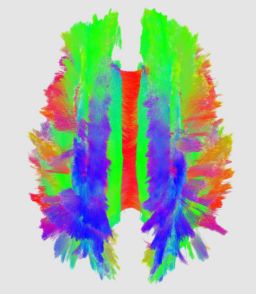
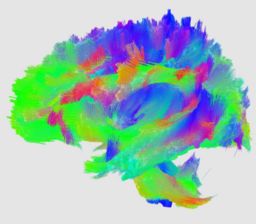
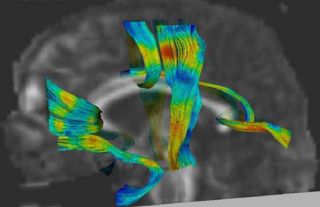
An initial test was performed by using the procedure on a set of images of healthy subject at age one year. The results of the tensor averaging are shown on the right. Tractography was also performed on the mean atlas image as shown.
Collaboration with PNL
We have begun to apply the DTI atlas building procedure to data provided by the PNL. A combined set of DTI scans from control and Schizophrenic subjects were aligned using the procedure described above. In the atlas space the SZ and CNTL groups are processed to produce voxel-wise statistics for each group. The figure below shows colored FA and mean diffusivity slices for both the CNTL and SZ group. Preliminary work is now being done on region of interest (ROI) hypothesis testing between the two populations.
Collaboration with MIT
During the Summer 2008 project week, we worked with the MIT group to incorporate b-spline groupwise registration into our atlas building procedure to construct a 100% open source atlas building toolkit. The results of this work appear on initial inspection to be similar in quality to that obtained with the fluid-based registration.
DTI Quantitative Tract Analysis
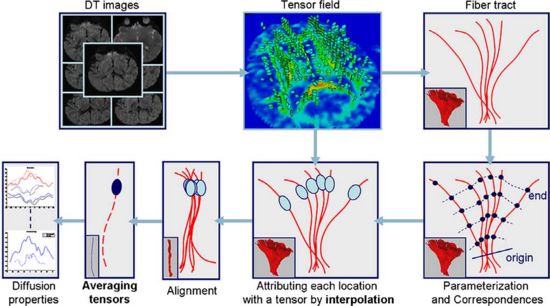
This project proposes a framework for quantitative analysis of DTI data. The framework uses the full tensor information for statistical analysis using the affine-invariant Riemannian metric for defining operations such as interpolation and averaging on tensors. Furtheremore, the results of tractography are used to provide a reference coordinate system the respresents the underlying structure of fiber bundles. The tract modeling framework includes a model both of the geometry of the fiber bundle and of the diffusion properties along the bundle. A new anisotropy measure called geodesic anisotropy (GA) is also included in the framework.
Group Analysis of tract properties
We have combined the procedure for atlas building of DTI with the tract analysis to provide a method for tract specific statistical analysis. This procedure is designed to do hypothesis testing and discrimination between two populations. The focus of the analysis is tract specific comparisons of diffusion properties such as fractional anisotropy (FA), mean diffusivity, etc rather than comparison of the shape or size of fiber tracts. The procedure works by combining all images from both populations into a single DTI atlas using the procedure described above. In the atlas, fibers are computed to create a template geometry for fiber tracts of interest. The transformations mapping each subject into the atlas are then used to map the diffusion statistics of interest onto the reference atlas fiber tract. This creates a set of fiber bundles, one for each subject, with identical geometry but differing diffusion properties. The tract analsysis procedure described above is then used to create a sampled function of these diffusion properties as a function of tract arc-length.
Statistical analysis of the sampled function requires the understanding the arc-length functions are sampled representations of a continuous underlying biology. Furthermore, diffusion statistics such as FA or MD may be highly correlated in the same voxel, and sampled locations along the tracts are likely to be highly spatially correlated. For these reasons, a method that operates on the space of continuous functions of the joint tensor properties is advantageous for statistical analysis. Our method fits b-spline basis functions to the sampled curves and performs PCA for data driven reduction of the dimensionality. Within the PCA coefficient space multi-variate analysis is performed using a permutation test based on the Hotelling T2 metric. This provides a method for performing a single global hypothesis test between the tracts of the two populations.
Software
- Algorithms written in ITK. GUI of prototype software written in QT (FiberViewer software). Prototype software tested in clinical studies at UNC. Validation tests with repeated DTI of same subject (6 cases). FiberTracking download
- Additionally available: ITK compatible fibertracking prototype tool FiberTracking to be used to study overlap/dissimilarity with other tools already available to NA-MIC: Functionality: reads raw DW-MRI data (6 direction Basser scheme), fiber tracking based on user-selected source and regions (S. Mori scheme), display of fibertracts and volumetric data, output: sets of streamlines in ITK polyline format attributedwith DTI properties and display parameteres (radiusof tubes, local color, etc.). FiberViewer download
- Command line tools for DTI processing available DWIProcess
Application to pediatric data
We have tested the analysis procedure on a dataset of pediatric development provided by John H Gilmore of UNC.
Key Investigators
- Utah Algorithms: Casey Goodlett, Isabelle Corouge, P. Thomas Fletcher, Guido Gerig
- Clinical Collaborators
- UNC: John H Gilmore
- PNL: Marek Kubicki, Sylvain Bouix
- Algorithm Collaborators
- MIT: Polina Golland, Serdar Balci
Publications
In Print