Difference between revisions of "Projects:SphericalDemons"
| Line 93: | Line 93: | ||
= Publications = | = Publications = | ||
| − | * [http://www.na-mic.org/publications/pages/display?search=Projects:SphericalDemons&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database] | + | * [http://www.na-mic.org/publications/pages/display?search=Projects:SphericalDemons&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Spherical Demons: Fast Surface Registration] |
[[Category: Registration]] [[Category:Segmentation]] | [[Category: Registration]] [[Category:Segmentation]] | ||
Latest revision as of 20:04, 11 May 2010
Home < Projects:SphericalDemonsBack to NA-MIC Collaborations, MIT Algorithms
Spherical Demons
We present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently approximated on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, the resulting registration is diffeomorphic and fast -- registration of two cortical mesh models with more than 100k nodes takes less than 5 minutes, comparable to the fastest surface registration algorithms. Moreover, the accuracy of our method compares favorably to the popular FreeSurfer registration algorithm. We validate the technique in two different settings: (1) parcellation in a set of in-vivo cortical surfaces and (2) Brodmann area localization in ex-vivo cortical surfaces.
Description
Motivated by the spherical representation of the cerebral cortex, this work deals with the problem of registering spherical images. Cortical folding patterns are correlated with both cytoarchitectural and functional regions. In group studies of cortical structure and function, determining corresponding folds across subjects is therefore important.
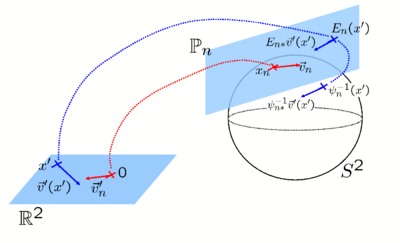
Unfortunately, many spherical warping algorithms are computationally expensive. One reason is the need for invertible deformations that preserve the topology of structural or functional regions across subjects. In this work, we take the approach, previously demonstrated in the Euclidean space [3], of restricting the deformation space to be a composition of diffeomorphisms, each of which is parameterized by a stationary velocity field. In each iteration, the algorithm greedily seeks the best diffeomorphism to be composed with the current transformation, resulting in much faster updates.
Another challenge in registration is the tradeoff between the image similarity measure and the regularization in the objective function. Since most regularizations favor smooth deformations, the gradient computation is complicated by the need to take into account the deformation in neighboring regions. For Euclidean images, the demons objective function facilitates a fast two-step optimization where the second step handles the warp regularization via a single convolution with a smoothing filter [2,3]. Based on spherical vector spline interpolation theory and other differential geometric tools, we show that the two-stage optimization procedure of the demons algorithm can be efficiently applied on the sphere.
Experimental Results
We use two sets of experiments to compare the accuracy of Spherical Demons and FreeSurfer [1]. The FreeSurfer registration algorithm uses the same similarity measure as Spherical Demons, but penalizes for metric and areal distortion. Its runtime is more than an hour while our runtime is less than 5 minutes.
(1) Parcellation of In-Vivo Cortical Surfaces
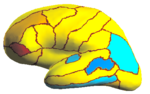
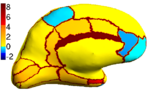
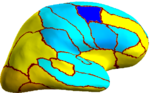
We consider a set of 39 left and right cortical surface models extracted from in-vivo MRI. Each surface is spherically parameterized and represented as a spherical image with geometric features at each vertex (e.g., sulcal depth and curvature). Both hemispheres are manually parcellated by a neuroanatomist into 35 major sulci and gyri. We validate our algorithm in the context of automatic cortical parcellation.
We co-register all 39 spherical images of cortical geometry with Spherical Demons by iteratively building an atlas and registering the surfaces to the atlas. The atlas consists of the mean and variance of cortical geometry. We then perform cross-validation parcellation 4 times, by leaving out subjects 1 to 10, training a classifier using the remaining subjects, and using it to classify subjects 1 to 10. We repeat with subjects 11-20, 21-30 and 31-39. We also perform registration and cross-validation with the FreeSurfer algorithm [1] using the same features and parcellation algorithm. Once again, the atlas consists of the mean and variance of cortical geometry.
The average Dice measure (defined as the ratio of cortical surface area with correct labels to the total surface area averaged over the test set) on the left hemisphere is 88.9 for FreeSurfer and 89.6 for Spherical Demons. While the improvement is not big, the
difference is statistically significant for a one-sided t-test with the Dice measure of each subject treated as an independent sample (p = 2e-6). On the right hemisphere, FreeSurfer obtains a Dice of 88.8 and Spherical Demons achieves 89.1. Here, the improvement is smaller, but still statistically significant (p = 0.01).
Because the average Dice can be deceiving by suppressing small structures, we analyze the segmentation accuracy per structure. On the left (right) hemisphere, the segmentations of 16 (8) structures are statistically significantly improved by Spherical Demons with respect to FreeSurfer, while no structure got worse (FDR = 0.05). The above figure shows the percentage improvement of individual structures. Parcellation results suggest that our registration is at least as accurate as FreeSurfer.
(2) Brodmann Areas Localization on Ex-vivo Cortical Surfaces
In this experiment, we evaluate the registration accuracy on ten human brains analyzed histologically postmortem. The histological sections were aligned to postmortem MR with nonlinear warps to build a 3D volume. Eight manually labeled Brodmann areas from histology were sampled onto each hemispheric surface model and sampling errors were manually corrected. Brodmann areas are cyto-architectonically defined regions closely related to cortical function.
It has been shown that nonlinear surface registration of cortical folds can significantly improve Brodmann area overlap across different subjects. Registering the ex-vivo surfaces is more difficult than in-vivo surfaces because the reconstructed volumes are extremely noisy, resulting in noisy geometric features.
We co-register the ten surfaces to each other by iteratively building an atlas and registering the surfaces to the atlas. We compute the average distance between the boundaries of the Brodmann areas for each pair of registered subjects. We perform a permutation test to test for statistical significance. Spherical Demons improves the alignment of 5 (2) Brodmann areas on the left (right) hemisphere (FDR = 0.05) compared with FreeSurfer and no structure gets worse. These results suggest that the Spherical Demons algorithm is at least as accurate as FreeSurfer in aligning Brodmann areas.
Code
Matlab code is currently available at http://yeoyeo02.googlepages.com/sphericaldemonsrelease
We are currently working in collaboration with Kitware to make the code available in ITK.
[1] B. Fischl, M. Sereno, R. Tootell, and A. Dale. High-resolution Intersubject Averaging and a Coordinate System for the Cortical Surface. Human Brain Mapping, 8(4):272–284, 1999.
[2] J. Thirion. Image Matching as a Diffusion Process: an Analogy with Maxwell’s Demons. Medical Image Analysis, 2(3):243–260, 1998.
[3] T. Vercauteren, X. Pennec, A. Perchant, and N. Ayache. Non-parametric Diffeomorphic Image Registration with the Demons Registration. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), volume 4792 of LNCS, pages 319–326, 2007.
Key Investigators
- MIT: [| B.T. Thomas Yeo], Mert Sabuncu, Polina Golland.
- Harvard: Bruce Fischl.
- INRIA: Nicholas Ayache.
- Mauna Kea Technologies: Tom Vercauteren.
- Kitware: Luis Ibanez, Michel Audette.