Difference between revisions of "Projects:GeodesicShapeRegression"
Jfishbaugh (talk | contribs) |
Jfishbaugh (talk | contribs) |
||
| Line 25: | Line 25: | ||
For details on the mathematical formulation and estimation of model parameters given observed data, see [1,2,3]. | For details on the mathematical formulation and estimation of model parameters given observed data, see [1,2,3]. | ||
| + | |||
| + | == Experimental Results for Shapes == | ||
| + | |||
| + | '''Pediatric Subcortical Development''' | ||
| + | |||
| + | We investigate the application of geodesic shape regression to model pediatric subcortical development. Three subcortical shapes are considered as a multi-object shape complex: putamen, amygdala, and hippocampus. The structures were obtained from MRI of a healthy child scanned at approximately 9, 13, and 24 months of age. Regression was conducted on all shapes simultaneously, resulting in one deformation of the ambient space. | ||
| + | |||
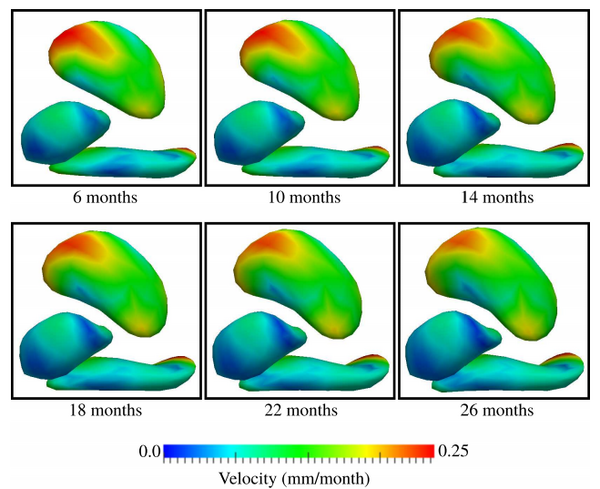
| + | Several snapshots of the evolution of subcortical structures is shown in Fig. 2, with estimated baseline shape shown at 6 months. From 6 to 26 months, all subcortical structures increase in size, with the putamen demonstrating the most dramatic growth. The evolution of the putamen is characterized by accelerated growth at the superior anterior and inferior posterior regions, while the hippocampus grows mostly at the extreme posterior region, expanding and bending at the tip. The geodesic model is able to capture interesting non-linear growth patterns with few parameters; the full time evolution is modeled by three baseline shapes and 126 momenta vectors. | ||
| + | |||
| + | [[File:Geodesic_subcort_panel.png|600px|center|thumb|'''Fig. 2.''' Snapshots of subcortical shape evolution after geodesic regression on a multi-object complex: putamen, amygdala, and hippocampus.]] | ||
| + | |||
| + | This experiment demonstrates the applicability of the geodesic model in characterizing pediatric subcortical development. Our regression framework simultaneously handles multiple shapes, including those with complex geometry. Multi-object regression allows for a more complete analysis, compared to an independent treatment of each subcortical structure, which ignores potentially important spatial relationships between structures. | ||
= Literature = | = Literature = | ||
Revision as of 03:52, 14 October 2014
Home < Projects:GeodesicShapeRegressionBack to Utah 2 Algorithms
Ongoing Work (Updated 10/2014)
Geodesic Regression for Anatomical Shape Complexes
Shape regression is of crucial importance for statistical shape analysis. It is useful to find correlations between shape configuration and a continuous scalar parameter such as age, disease progression, drug delivery, or cognitive scores. When only few follow-up observations are available, regression is also a necessary tool to interpolate between data points and provide a scenario of continuous shape evolution over the parameter range. Longitudinal studies also require to compare such regressions across different subjects.
Multi-Object Shape Complexes
Medical imaging data is available in many formats. From volumetric imaging data, anatomical structures are extracted. The structures can be represented in several ways (in 2D or 3D): triangular meshes for surfaces, landmarks, point clouds, curves, etc. It is important to consider image data in anatomical context, which motivates regression on image and shape data in different combinations (a multi-object complex).
Geodesic Growth Model
The geodesic regression model leverages image and shape data together to estimate a single time-dependent deformation of the ambient space. By analogy with linear regression, we estimate a baseline shape configuration (intercept) and deformation parameters (slope) in order to minimize the distance between the model and the observed shapes.
The deformations in our model are diffeomorphisms (smooth, one-to-one, and invertible transformation of space) which act on shapes embedded in the ambient 2D or 3D space. The group of diffeomorphisms forms an infinite dimensional manifold. This is the space in which our model is geodesic, a minimal energy curve on the manifold where each point along the curve is a diffeomorphism.
We call this continuous curve of diffeomorphisms a geodesic flow of diffeomorphisms, which is conveniently parameterized through a tangent space representation. The geodesic is fully described by a vector field in Euclidean space (the tangent space at a point on the manifold), called the initial momenta. From initial momenta, we can travel along the geodesic and construct diffeomorphisms by solving a system of coupled ODEs. The flow of diffeomorphisms act continuously on the embedded shapes, starting with the baseline shape configuration, resulting in continuous shape trajectories.
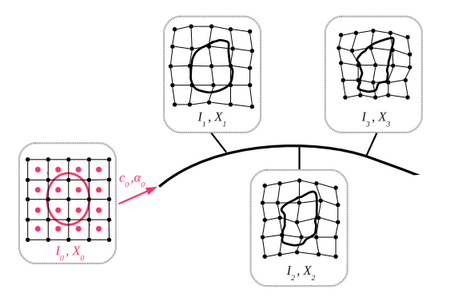
Therefore, the model is fully parameterized by an initial baseline shape configuration (intercept) and initial momenta (slope). Model estimation consists of estimating a baseline shape configuration, initial momenta as well as their spatial locations, called control points. The control point formulation allows momenta to be located in areas which undergo the most dynamic changes, rather than being restricted by any particular shape representation, located at the voxels of the image for instance. A graphical overview of geodesic regression is shown in Fig. 1.
For details on the mathematical formulation and estimation of model parameters given observed data, see [1,2,3].
Experimental Results for Shapes
Pediatric Subcortical Development
We investigate the application of geodesic shape regression to model pediatric subcortical development. Three subcortical shapes are considered as a multi-object shape complex: putamen, amygdala, and hippocampus. The structures were obtained from MRI of a healthy child scanned at approximately 9, 13, and 24 months of age. Regression was conducted on all shapes simultaneously, resulting in one deformation of the ambient space.
Several snapshots of the evolution of subcortical structures is shown in Fig. 2, with estimated baseline shape shown at 6 months. From 6 to 26 months, all subcortical structures increase in size, with the putamen demonstrating the most dramatic growth. The evolution of the putamen is characterized by accelerated growth at the superior anterior and inferior posterior regions, while the hippocampus grows mostly at the extreme posterior region, expanding and bending at the tip. The geodesic model is able to capture interesting non-linear growth patterns with few parameters; the full time evolution is modeled by three baseline shapes and 126 momenta vectors.
This experiment demonstrates the applicability of the geodesic model in characterizing pediatric subcortical development. Our regression framework simultaneously handles multiple shapes, including those with complex geometry. Multi-object regression allows for a more complete analysis, compared to an independent treatment of each subcortical structure, which ignores potentially important spatial relationships between structures.
Literature
[1] Fishbaugh, J., Prastawa, M., Gerig, G., Durrleman, S. Geodesic regression of image and shape data for improved modeling of 4D trajectories. IEEE International Symposium on Biomedical Imaging (ISBI '14)
[2] Fishbaugh, J., Prastawa, M., Gerig, G., Durrleman, S. Geodesic image regression with a sparse parameterization of diffeomorphisms. Geometric Science of Information (GSI '13). LNCS vol 8085, pp. 95-102. (2013)
[3] Fishbaugh, J., Prastawa, M., Gerig, G., Durrleman, S. Geodesic shape regression in the framework of currents. Proc. of Information Processing in Medical Imaging (IPMI '13). Vol 23, pp. 718-729. (2013)
Key Investigators
- Utah: James Fishbaugh, Marcel Prastawa, Guido Gerig
- INRIA/ICM, Pitie Salpetriere Hospital: Stanley Durrleman