Difference between revisions of "Algorithm:MIT"
m (Fix MediaWiki table formatting issue discovered while converting to GitHub Flavored Markdown using pandoc (via https://github.com/outofcontrol/mediawiki-to-gfm)) Tag: 2017 source edit |
|||
| (385 intermediate revisions by 21 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to [[Algorithm:Main|NA-MIC Algorithms]] | + | Back to [[Algorithm:Main|NA-MIC Algorithms]] |
__NOTOC__ | __NOTOC__ | ||
| − | = Overview of MIT Algorithms = | + | = Overview of MIT Algorithms (PI: Polina Golland) = |
Our group seeks to model statistical variability of anatomy and function across subjects and between populations and to utilize computational models of such variability to improve predictions for individual subjects, as well as characterize populations. Our long-term goal is to develop methods for joint modeling of anatomy and function and to apply them in clinical and scientific studies. We work primarily with anatomical, DTI and fMRI images. We actively contribute implementations of our algorithms to the NAMIC-kit. | Our group seeks to model statistical variability of anatomy and function across subjects and between populations and to utilize computational models of such variability to improve predictions for individual subjects, as well as characterize populations. Our long-term goal is to develop methods for joint modeling of anatomy and function and to apply them in clinical and scientific studies. We work primarily with anatomical, DTI and fMRI images. We actively contribute implementations of our algorithms to the NAMIC-kit. | ||
| Line 7: | Line 7: | ||
= MIT Projects = | = MIT Projects = | ||
| − | {| cellpadding="10" | + | {| cellpadding="10" style="text-align:left;" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | <font color="red">'''New: '''</font> | + | || [[Image:Segmentation_example2.png|250px]] |
| + | || | ||
| + | |||
| + | == [[Projects:NonparametricSegmentation| Nonparametric Models for Supervised Image Segmentation]] == | ||
| + | |||
| + | We propose a non-parametric, probabilistic model for the automatic segmentation of medical images, | ||
| + | given a training set of images and corresponding label maps. The resulting inference algorithms we | ||
| + | develop rely on pairwise registrations between the test image and individual training images. The | ||
| + | training labels are then transferred to the test image and fused to compute a final segmentation of | ||
| + | the test subject. [[Projects:NonparametricSegmentation|More...]] | ||
| + | |||
| + | <font color="red">'''New: '''</font> | ||
| + | C. Wachinger and P. Golland. Spectral Label Fusion. In Proc. MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervenion, LNCS 7512:410-417, 2012. | ||
| + | |||
| + | |||
| + | |||
| + | |- | ||
| + | |||
| + | || [[Image:Mdepa_scar_DE-MRI_projection.png| 250px]] | ||
| + | || | ||
| + | |||
| + | == [[Projects:CardiacAblation | Segmentation and Visualization for Cardiac Ablation Procedures]] == | ||
| + | |||
| + | Catheter radio-frequency (RF) ablation is a technique used to treat atrial fibrillation, a very common heart condition. The objective of this project is to provide automatic segmentation and visualization tools to aid in the planning and outcome evaluation of cardiac ablation procedures. Specifically, we develop methods for the automatic segmentation of the left atrium of the heart and visualization of the ablation scars resulting from the procedure in clinical MR images. | ||
| + | [[Projects:CardiacAblation|More...]] | ||
| + | |||
| + | <font color="red">'''New: '''</font> | ||
| + | C. Wachinger and P. Golland. Spectral Label Fusion. In Proc. MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervenion, LNCS 7512:410-417, 2012. | ||
| + | |||
| + | |- | ||
| + | |||
| + | || [[Image:NetworkBrain.png|center|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:GenerativeBrainConnectivity|Generative Models of Brain Connectivity]] == | ||
| + | |||
| + | Our goal is to use measures of connectivity between various ROIs as an avenue for understanding the structural and functional effects of pathology. We assess functional and anatomical connectivity using both fMRI correlations and DWI tractography measures, respectively. Our methods are evaluated on a clinical study of schizophrenia. [[Projects:GenerativeBrainConnectivity|More...]] | ||
| + | |||
| + | <font color="red">'''New: '''</font> | ||
| + | A. Venkataraman, Y. Rathi, M. Kubicki, C.-F. Westin, and P. Golland. Joint Modeling of Anatomical and Functional Connectivity for Population Studies. IEEE Transactions on Medical Imaging, 31(2):164-182, 2012. | ||
| + | |||
| + | <font color="red">'''New: '''</font> A. Venkataraman, M. Kubicki and P. Golland. From Brain Connectivity Models to Identifying Foci of a Neurological Disorder. In Proc. MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention, LNCS 7510:715-722, 2012. | ||
| + | |||
| + | |- | ||
| + | |||
| + | || [[Image:GI_15_p05_orig.png|center| 200px]] | ||
| + | || | ||
| + | |||
| + | == [[Projects:DataDrivenFunctionalConnectivity|Data Driven Analysis of Functional Connectivity]] == | ||
| + | This project uses standard machine learning algorithms to automatically identify relevant patterns in functional connectivity data. Our first application is to determine predictive differences between a control and clinical population. Our second application is to partition the brain into different functional systems. [[Projects:DataDrivenFunctionalConnectivity|More...]] | ||
| + | |||
| + | <font color="red">'''New: '''</font> A. Venkataraman, T.J. Whitford, C-F. Westin, P. Golland and M. Kubicki. Whole Brain Resting State Functional Connectivity Abnormalities in Schizophrenia. Schizophrenia Research, 139(1-3):7-12, 2012. | ||
| + | |||
| + | |- | ||
| + | |||
| + | |||
| + | || [[Image:georgehc_disc_front.png|250px]] | ||
| + | || | ||
| + | |||
| + | == [[Projects:ModelingFunctionalActivationPatterns| Modeling Functional Activation Patterns]] == | ||
| + | |||
| + | For a given cognitive task such as language processing, the location of corresponding functional regions in the brain may vary across subjects relative to anatomy. We present a probabilistic generative model that accounts for such variability as observed in functional magnetic resonance imaging (fMRI) data. We relate our approach to sparse coding that estimates a basis consisting of functional regions in the brain. Individual fMRI data is represented as a weighted sum of these functional regions that undergo deformations. We demonstrate the proposed method on a language fMRI study. Our method identified activation regions that agree with known literature on language processing and established correspondences among activation regions across subjects, producing more robust group-level effects than anatomical alignment alone. [[Projects:ModelingFunctionalActivationPatterns|More...]] | ||
| + | |||
| + | <font color="red">'''New: '''</font> G. Chen, E. Fedorenko, N.G. Kanwisher, and P. Golland. Deformation-Invariant Sparse Coding for Modeling Spatial Variability of Functional Patterns in the Brain. In Proc. Neural Information Processing Systems (NIPS) Workshop on Machine Learning and Interpretation in Neuroimaging, LNAI 7263:68-75, 2012. | ||
| + | |||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:mit_fmri_clustering_parcellation2_xsub.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:fMRIClustering|Improving fMRI Analysis using Supervised and Unsupervised Learning]] == | ||
| + | |||
| + | One of the major goals in the analysis of fMRI data is the detection of networks in the brain with similar functional behavior. A wide variety of methods including hypothesis-driven statistical tests, supervised, and unsupervised learning methods have been employed to find these networks. In this project, we develop novel learning algorithms that enable more efficient inferences from fMRI measurements. [[Projects:fMRIClustering|More...]] | ||
| + | |||
| + | <font color="red">'''New: '''</font> E. Vul, D. Lashkari, P.-J. Hsieh, P. Golland; N.G. Kanwisher. Data-driven functional clustering reveals dominance of face, place, and body selectivity in the ventral visual pathway. Journal of Neurophysiology, 108:2306-2322, 2012. | ||
| + | |||
| + | <font color="red">'''New: '''</font> D. Lashkari, R. Sridharan, E. Vul, P.-J. Hsieh, N.G. Kanwisher, and P. Golland. Search for Patterns of Functional Specificity in the Brain: A Nonparametric Hierarchical Bayesian Model for Group fMRI Data. NeuroImage, 59(2):1348-1368, 2012. | ||
| + | |||
| + | |- | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | | | [[Image:NerveSegRes1.jpg|center| 200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:NerveSegmentation|Segmentation of Nerve and Nerve Ganglia in the Spine]] == | ||
| + | Automatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task. [[Projects:NerveSegmentation|More...]] | ||
| + | |||
| + | |||
| + | |- | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | | | [[Image:Atlas_OneCluster.png|center| 200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:ConnectivityAtlas| Functional connectivity atlases and tumors]] == | ||
| + | We learn an atlas of the functional connectivity structure that emerges during a cognitive process from a group of individuals. The atlas is a group-wise generative model that describes the fMRI responses of all subjects in the embedding space. The atlas is not directly coupled to the anatomical space, and can represent functional networks that are variable in their spatial distribution. | ||
| + | [[Projects:ConnectivityAtlas|More...]] | ||
| + | |||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:GiniContrast_Icon.png|center| 150px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:GiniContrast| Multi-variate activation detection]] == | ||
| + | We study and demonstrate the benefits of Random Forest classifiers and the associated Gini importance measure for selecting voxel subsets that form a mul- tivariate neural response. The method does not rely on a priori assumptions about the signal distribution, a specific statistical or functional model or regularization. Instead it uses the predictive power of features to characterize their relevance for encoding task information. | ||
| + | [[Projects:GiniContrast|More...]] | ||
| + | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:BjoernTumor3.png|center|200px]] |
| | | | | | ||
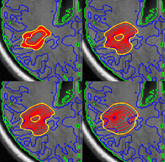
| − | == [[Projects: | + | == [[Projects:TumorModeling|Brain Tumor Segmentation and Modeling]] == |
| − | We | + | We are interested in developing computational methods for the assimilation of magnetic resonance image data into physiological models of glioma - the most frequent primary brain tumor - for a patient-adaptive modeling of tumor growth. [[Projects:TumorModeling|More...]] |
| − | [[Projects: | ||
| − | |||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | |
| + | | | [[Image:Namic wiki.png|200px]] | ||
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:QuantitativeSusceptibilityMapping| Quantitative Susceptibility Mapping ]] == |
| + | |||
| + | There is increasing evidence that excessive iron deposition in specific regions | ||
| + | of the brain is associated with neurodegenerative disorders such as Alzheimer's | ||
| + | and Parkinson's disease. The role of iron in the pathogenesis of these diseases | ||
| + | remains unknown and is difficult to determine without a non-invasive method | ||
| + | to quantify its concentration in-vivo. Since iron is a ferromagnetic substance, | ||
| + | changes in iron concentration result in local changes in the magnetic susceptibility of tissue. | ||
| + | In magnetic resonance imaging (MRI) experiments, differences | ||
| + | in magnetic susceptibility cause perturbations in the local magnetic field, which | ||
| + | can be computed from the phase of the MR signal. [[Projects:QuantitativeSusceptibilityMapping|More...]] | ||
| + | |||
| + | |- | ||
| + | | | [[Image:TGIt.gif|center| 150px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:LatentAtlasSegmentation|Joint Segmentation of Image Ensembles via Latent Atlases]] == | ||
| + | |||
| + | Spatial priors, such as probabilistic atlases, play an important role in MRI segmentation. The atlases are typically generated by averaging manual labels of aligned brain regions across different subjects. However, the availability of comprehensive, reliable and suitable manual segmentations is limited. We therefore propose a joint segmentation of corresponding, aligned structures in the entire population that does not require a probability atlas. | ||
| + | [[Projects:LatentAtlasSegmentation|More...]] | ||
| + | |||
| + | |- | ||
| + | |||
| + | || [[Image:lh.pm14686.BA2.gif|250px]] | ||
| + | || | ||
| + | |||
| + | == [[Projects:LearningRegistrationCostFunctions| Learning Task-Optimal Registration Cost Functions]] == | ||
| + | |||
| + | We present a framework for learning the parameters of registration cost functions. The parameters of the registration cost function -- for example, the tradeoff between the image similarity and regularization terms -- are typically determined manually through inspection of the image alignment and then fixed for all applications. We propose a principled approach to learn these parameters with respect to particular applications. [[Projects:LearningRegistrationCostFunctions|More...]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:CoordinateChart.png|250px]] |
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:SphericalDemons|Spherical Demons: Fast Surface Registration]] == |
| − | We | + | We present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently approximated on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, [[Projects:SphericalDemons|More...]] |
| − | [[Projects: | ||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | |
| + | |||
| + | | | [[Image:FMRIEvaluationchart.jpg|200px]] | ||
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:fMRIDetection|fMRI Detection and Analysis]] == |
| + | |||
| + | We are exploring algorithms for improved fMRI detection and interpretation by incorporting spatial priors and anatomical information to guide the detection. [[Projects:fMRIDetection|More...]] | ||
| + | |||
| + | |- | ||
| + | |||
| + | |||
| + | | | [[Image:epi_correction_small.jpg|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:FieldmapFreeDistortionCorrection|Fieldmap-Free EPI Distortion Correction]] == | ||
| + | |||
| + | In this project we aim to improve the EPI distortion correction algorithms. [[Projects:FieldmapFreeDistortionCorrection|More...]] | ||
| + | |||
| + | |- | ||
| + | |||
| + | || [[Image:TetrahedralAtlasWarp.gif |250px]] | ||
| + | || | ||
| − | + | == [[Projects:BayesianMRSegmentation| Bayesian Segmentation of MRI Images]] == | |
| − | + | The aim of this project is to develop, implement, and validate a generic method for segmenting MRI images that automatically adapts to different acquisition sequences. [[Projects:BayesianMRSegmentation|More...]] | |
| − | |||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:ICluster_templates.gif|250px]] |
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:MultimodalAtlas|Multimodal Atlas]] == |
| − | In this | + | In this work, we propose and investigate an algorithm that jointly co-registers a collection of images while computing multiple templates. The algorithm, called '''iCluster''', is used to compute multiple atlases for a given population. |
| + | [[Projects:MultimodalAtlas|More...]] | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:GroupwiseSummary.PNG|200px]] |
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:GroupwiseRegistration|Groupwise Registration]] == |
| − | + | We extend a previously demonstrated entropy based groupwise registration method to include a free-form deformation model based on B-splines. We provide an efficient implementation using stochastic gradient descents in a multi-resolution setting. We demonstrate the method in application to a set of 50 MRI brain scans and compare the results to a pairwise approach using segmentation labels to evaluate the quality of alignment. | |
| − | + | In a related project, we develop a method that reconciles the practical advantages of symmetric registration with the asymmetric nature of image-template registration by adding a simple correction factor to the symmetric cost function. We instantiate our model within a log-domain diffeomorphic registration framework. Our experiments show exploiting the asymmetry in image-template registration improves alignment in the image coordinates. [[Projects:GroupwiseRegistration|More...]] | |
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:JointRegSeg.png|200px]] |
| | | | | | ||
| + | == [[Projects:RegistrationRegularization|Optimal Atlas Regularization in Image Segmentation]] == | ||
| + | |||
| + | We propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas in a segmentation application. | ||
| + | [[Projects:RegistrationRegularization|More...]] | ||
| + | |- | ||
| − | + | | | [[Image:FoldingSpeedDetection.png|150px|]] | |
| + | | | | ||
| − | + | == [[Projects:ShapeAnalysisWithOvercompleteWavelets|Shape Analysis With Overcomplete Wavelets]] == | |
| − | + | In this work, we extend the Euclidean wavelets to the sphere. The resulting over-complete spherical wavelets are invariant to the rotation of the spherical image parameterization. We apply the over-complete spherical wavelet to cortical folding development [[Projects:ShapeAnalysisWithOvercompleteWavelets|More...]] | |
|- | |- | ||
| Line 110: | Line 259: | ||
== [[Projects:DTIModeling|Fiber Tract Modeling, Clustering, and Quantitative Analysis]] == | == [[Projects:DTIModeling|Fiber Tract Modeling, Clustering, and Quantitative Analysis]] == | ||
| − | The goal of this work is to model the shape of the fiber bundles and use this model | + | The goal of this work is to model the shape of the fiber bundles and use this model description in clustering and statistical analysis of fiber tracts. [[Projects:DTIModeling|More...]] |
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:Progress_Registration_Segmentation_Shape.jpg|180px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:ShapeBasedSegmentationAndRegistration|Shape Based Segmentation and Registration]] == | ||
| + | |||
| + | This type of algorithm assigns a tissue type to each voxel in the volume. Incorporating prior shape information biases the label assignment towards contiguous regions that are consistent with the shape model. [[Projects:ShapeBasedSegmentationAndRegistration|More...]] | ||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:MIT_DTI_JointSegReg_atlas3D.jpg|200px]] |
| + | | | | ||
| + | |||
| + | == [[Projects:DTIFiberRegistration|Joint Registration and Segmentation of DWI Fiber Tractography]] == | ||
| + | |||
| + | The goal of this work is to jointly register and cluster DWI fiber tracts obtained from a group of subjects. [[Projects:DTIFiberRegistration|More...]] | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:brain.png|200px]] | ||
| | | | | | ||
| − | == [[Projects: | + | == [[Projects:DTIClustering|DTI Fiber Clustering and Fiber-Based Analysis]] == |
| − | + | The goal of this project is to provide structural description of the white matter architecture as a partition into coherent fiber bundles and clusters, and to use these bundles for quantitative measurement. [[Projects:DTIClustering|More...]] | |
| − | |||
|- | |- | ||
| Line 136: | Line 299: | ||
Unlike conventional MRI, DTI provides adequate contrast to segment the thalamic nuclei, which are gray matter structures. [[Projects:DTISegmentation|More...]] | Unlike conventional MRI, DTI provides adequate contrast to segment the thalamic nuclei, which are gray matter structures. [[Projects:DTISegmentation|More...]] | ||
| − | |||
| − | |||
|- | |- | ||
| Line 156: | Line 317: | ||
Our goal is to develop mathematical approaches to modeling anatomical variability within and across populations using tools like local shape descriptors of specific regions of interest and global constellation descriptors of multiple ROI's. [[Projects:ShapeAnalysis|More...]] | Our goal is to develop mathematical approaches to modeling anatomical variability within and across populations using tools like local shape descriptors of specific regions of interest and global constellation descriptors of multiple ROI's. [[Projects:ShapeAnalysis|More...]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
Latest revision as of 06:17, 11 April 2023
Home < Algorithm:MITBack to NA-MIC Algorithms
Overview of MIT Algorithms (PI: Polina Golland)
Our group seeks to model statistical variability of anatomy and function across subjects and between populations and to utilize computational models of such variability to improve predictions for individual subjects, as well as characterize populations. Our long-term goal is to develop methods for joint modeling of anatomy and function and to apply them in clinical and scientific studies. We work primarily with anatomical, DTI and fMRI images. We actively contribute implementations of our algorithms to the NAMIC-kit.
MIT Projects
|
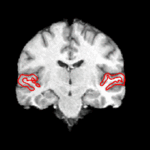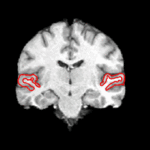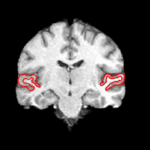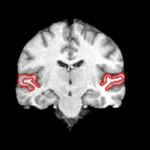
Nonparametric Models for Supervised Image SegmentationWe propose a non-parametric, probabilistic model for the automatic segmentation of medical images, given a training set of images and corresponding label maps. The resulting inference algorithms we develop rely on pairwise registrations between the test image and individual training images. The training labels are then transferred to the test image and fused to compute a final segmentation of the test subject. More... New: C. Wachinger and P. Golland. Spectral Label Fusion. In Proc. MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervenion, LNCS 7512:410-417, 2012.
|
|
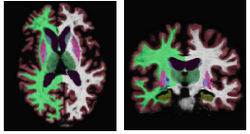
Segmentation and Visualization for Cardiac Ablation ProceduresCatheter radio-frequency (RF) ablation is a technique used to treat atrial fibrillation, a very common heart condition. The objective of this project is to provide automatic segmentation and visualization tools to aid in the planning and outcome evaluation of cardiac ablation procedures. Specifically, we develop methods for the automatic segmentation of the left atrium of the heart and visualization of the ablation scars resulting from the procedure in clinical MR images. More... New: C. Wachinger and P. Golland. Spectral Label Fusion. In Proc. MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervenion, LNCS 7512:410-417, 2012. |
Generative Models of Brain ConnectivityOur goal is to use measures of connectivity between various ROIs as an avenue for understanding the structural and functional effects of pathology. We assess functional and anatomical connectivity using both fMRI correlations and DWI tractography measures, respectively. Our methods are evaluated on a clinical study of schizophrenia. More... New: A. Venkataraman, Y. Rathi, M. Kubicki, C.-F. Westin, and P. Golland. Joint Modeling of Anatomical and Functional Connectivity for Population Studies. IEEE Transactions on Medical Imaging, 31(2):164-182, 2012. New: A. Venkataraman, M. Kubicki and P. Golland. From Brain Connectivity Models to Identifying Foci of a Neurological Disorder. In Proc. MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention, LNCS 7510:715-722, 2012. | |
Data Driven Analysis of Functional ConnectivityThis project uses standard machine learning algorithms to automatically identify relevant patterns in functional connectivity data. Our first application is to determine predictive differences between a control and clinical population. Our second application is to partition the brain into different functional systems. More... New: A. Venkataraman, T.J. Whitford, C-F. Westin, P. Golland and M. Kubicki. Whole Brain Resting State Functional Connectivity Abnormalities in Schizophrenia. Schizophrenia Research, 139(1-3):7-12, 2012. | |
|
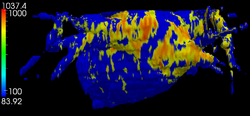
Modeling Functional Activation PatternsFor a given cognitive task such as language processing, the location of corresponding functional regions in the brain may vary across subjects relative to anatomy. We present a probabilistic generative model that accounts for such variability as observed in functional magnetic resonance imaging (fMRI) data. We relate our approach to sparse coding that estimates a basis consisting of functional regions in the brain. Individual fMRI data is represented as a weighted sum of these functional regions that undergo deformations. We demonstrate the proposed method on a language fMRI study. Our method identified activation regions that agree with known literature on language processing and established correspondences among activation regions across subjects, producing more robust group-level effects than anatomical alignment alone. More... New: G. Chen, E. Fedorenko, N.G. Kanwisher, and P. Golland. Deformation-Invariant Sparse Coding for Modeling Spatial Variability of Functional Patterns in the Brain. In Proc. Neural Information Processing Systems (NIPS) Workshop on Machine Learning and Interpretation in Neuroimaging, LNAI 7263:68-75, 2012.
|
|
Improving fMRI Analysis using Supervised and Unsupervised LearningOne of the major goals in the analysis of fMRI data is the detection of networks in the brain with similar functional behavior. A wide variety of methods including hypothesis-driven statistical tests, supervised, and unsupervised learning methods have been employed to find these networks. In this project, we develop novel learning algorithms that enable more efficient inferences from fMRI measurements. More... New: E. Vul, D. Lashkari, P.-J. Hsieh, P. Golland; N.G. Kanwisher. Data-driven functional clustering reveals dominance of face, place, and body selectivity in the ventral visual pathway. Journal of Neurophysiology, 108:2306-2322, 2012. New: D. Lashkari, R. Sridharan, E. Vul, P.-J. Hsieh, N.G. Kanwisher, and P. Golland. Search for Patterns of Functional Specificity in the Brain: A Nonparametric Hierarchical Bayesian Model for Group fMRI Data. NeuroImage, 59(2):1348-1368, 2012. |
Segmentation of Nerve and Nerve Ganglia in the SpineAutomatic segmentation of neural tracts in the dural sac and outside of the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves in high resolution MR images makes segmentation a challenging task. More...
| |
Functional connectivity atlases and tumorsWe learn an atlas of the functional connectivity structure that emerges during a cognitive process from a group of individuals. The atlas is a group-wise generative model that describes the fMRI responses of all subjects in the embedding space. The atlas is not directly coupled to the anatomical space, and can represent functional networks that are variable in their spatial distribution. More...
| |
Multi-variate activation detectionWe study and demonstrate the benefits of Random Forest classifiers and the associated Gini importance measure for selecting voxel subsets that form a mul- tivariate neural response. The method does not rely on a priori assumptions about the signal distribution, a specific statistical or functional model or regularization. Instead it uses the predictive power of features to characterize their relevance for encoding task information. More...
| |
Brain Tumor Segmentation and ModelingWe are interested in developing computational methods for the assimilation of magnetic resonance image data into physiological models of glioma - the most frequent primary brain tumor - for a patient-adaptive modeling of tumor growth. More... | |
|
Quantitative Susceptibility MappingThere is increasing evidence that excessive iron deposition in specific regions of the brain is associated with neurodegenerative disorders such as Alzheimer's and Parkinson's disease. The role of iron in the pathogenesis of these diseases remains unknown and is difficult to determine without a non-invasive method to quantify its concentration in-vivo. Since iron is a ferromagnetic substance, changes in iron concentration result in local changes in the magnetic susceptibility of tissue. In magnetic resonance imaging (MRI) experiments, differences in magnetic susceptibility cause perturbations in the local magnetic field, which can be computed from the phase of the MR signal. More... |
Joint Segmentation of Image Ensembles via Latent AtlasesSpatial priors, such as probabilistic atlases, play an important role in MRI segmentation. The atlases are typically generated by averaging manual labels of aligned brain regions across different subjects. However, the availability of comprehensive, reliable and suitable manual segmentations is limited. We therefore propose a joint segmentation of corresponding, aligned structures in the entire population that does not require a probability atlas. More... | |
|
Learning Task-Optimal Registration Cost FunctionsWe present a framework for learning the parameters of registration cost functions. The parameters of the registration cost function -- for example, the tradeoff between the image similarity and regularization terms -- are typically determined manually through inspection of the image alignment and then fixed for all applications. We propose a principled approach to learn these parameters with respect to particular applications. More...
|
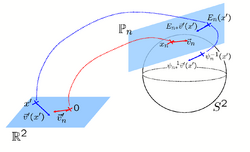
|
Spherical Demons: Fast Surface RegistrationWe present the fast Spherical Demons algorithm for registering two spherical images. By exploiting spherical vector spline interpolation theory, we show that a large class of regularizers for the modified demons objective function can be efficiently approximated on the sphere using convolution. Based on the one parameter subgroups of diffeomorphisms, More...
|
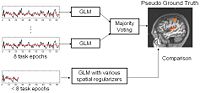
|
fMRI Detection and AnalysisWe are exploring algorithms for improved fMRI detection and interpretation by incorporting spatial priors and anatomical information to guide the detection. More... |
|
Fieldmap-Free EPI Distortion CorrectionIn this project we aim to improve the EPI distortion correction algorithms. More... |
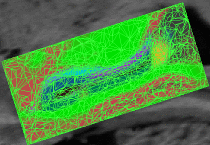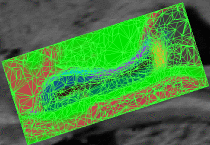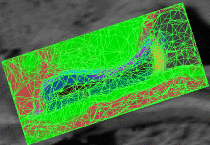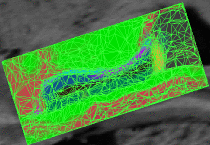
|
Bayesian Segmentation of MRI ImagesThe aim of this project is to develop, implement, and validate a generic method for segmenting MRI images that automatically adapts to different acquisition sequences. More... |
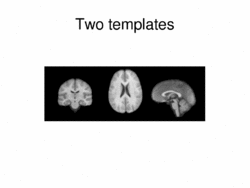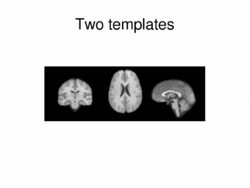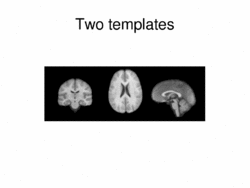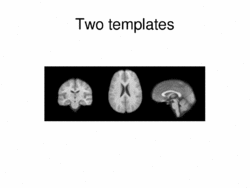
|
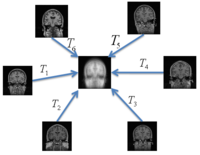
Multimodal AtlasIn this work, we propose and investigate an algorithm that jointly co-registers a collection of images while computing multiple templates. The algorithm, called iCluster, is used to compute multiple atlases for a given population. More... |
|
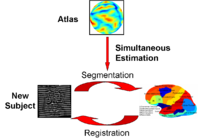
Groupwise RegistrationWe extend a previously demonstrated entropy based groupwise registration method to include a free-form deformation model based on B-splines. We provide an efficient implementation using stochastic gradient descents in a multi-resolution setting. We demonstrate the method in application to a set of 50 MRI brain scans and compare the results to a pairwise approach using segmentation labels to evaluate the quality of alignment. In a related project, we develop a method that reconciles the practical advantages of symmetric registration with the asymmetric nature of image-template registration by adding a simple correction factor to the symmetric cost function. We instantiate our model within a log-domain diffeomorphic registration framework. Our experiments show exploiting the asymmetry in image-template registration improves alignment in the image coordinates. More... |
|
Optimal Atlas Regularization in Image SegmentationWe propose a unified framework for computing atlases from manually labeled data sets at various degrees of “sharpness” and the joint registration and segmentation of a new brain with these atlases. Using this framework, we investigate the tradeoff between warp regularization and image fidelity, i.e. the smoothness of the new subject warp and the sharpness of the atlas in a segmentation application. More... |
|
Shape Analysis With Overcomplete WaveletsIn this work, we extend the Euclidean wavelets to the sphere. The resulting over-complete spherical wavelets are invariant to the rotation of the spherical image parameterization. We apply the over-complete spherical wavelet to cortical folding development More... |
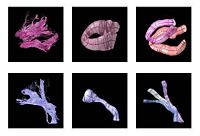
|
Fiber Tract Modeling, Clustering, and Quantitative AnalysisThe goal of this work is to model the shape of the fiber bundles and use this model description in clustering and statistical analysis of fiber tracts. More... |
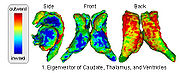
|
Shape Based Segmentation and RegistrationThis type of algorithm assigns a tissue type to each voxel in the volume. Incorporating prior shape information biases the label assignment towards contiguous regions that are consistent with the shape model. More...
|

|
Joint Registration and Segmentation of DWI Fiber TractographyThe goal of this work is to jointly register and cluster DWI fiber tracts obtained from a group of subjects. More... |
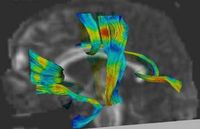
|
DTI Fiber Clustering and Fiber-Based AnalysisThe goal of this project is to provide structural description of the white matter architecture as a partition into coherent fiber bundles and clusters, and to use these bundles for quantitative measurement. More...
|
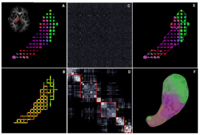
|
DTI-based SegmentationUnlike conventional MRI, DTI provides adequate contrast to segment the thalamic nuclei, which are gray matter structures. More... |
|
Stochastic TractographyThis work calculates posterior distributions of white matter fiber tract parameters given diffusion observations in a DWI volume. More... |
|
Population Analysis of Anatomical VariabilityOur goal is to develop mathematical approaches to modeling anatomical variability within and across populations using tools like local shape descriptors of specific regions of interest and global constellation descriptors of multiple ROI's. More... |