Difference between revisions of "Projects:OptimalMassTransportRegistration"
| (21 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Back to | + | Back to [[Algorithm:Stony Brook|Stony Brook University Algorithms]] |
__NOTOC__ | __NOTOC__ | ||
= Optimal Mass Transport = | = Optimal Mass Transport = | ||
| Line 16: | Line 16: | ||
# The algorithm is designed to take into account changes in densities that result from changes in area or volume. | # The algorithm is designed to take into account changes in densities that result from changes in area or volume. | ||
| − | + | == Algorithm == | |
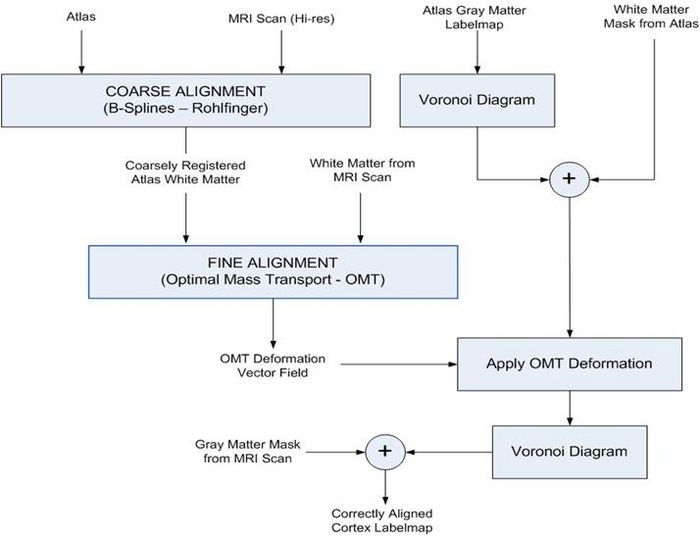
The flowchart of the algorithm is shown in the following figure. | The flowchart of the algorithm is shown in the following figure. | ||
| Line 24: | Line 24: | ||
<br/> | <br/> | ||
| − | + | == Multi-resolution Approach == | |
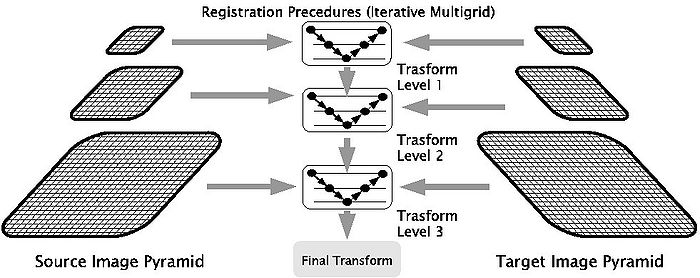
Performing image registration using a multi-resolution approach is widely used to improve speed, accuracy and robustness. Registration is first performed at a coarse scale. The spatial mapping determined at coarse scale is then used to initialize registration at the next finer scale. This process is repeated until it reaches the finest scale. Our coarse-to-fine hierarchy comprises of three levels and we use bi-cubic interpolation to interpolate results from coarse to fine grid. This process is depicted in the following figure. | Performing image registration using a multi-resolution approach is widely used to improve speed, accuracy and robustness. Registration is first performed at a coarse scale. The spatial mapping determined at coarse scale is then used to initialize registration at the next finer scale. This process is repeated until it reaches the finest scale. Our coarse-to-fine hierarchy comprises of three levels and we use bi-cubic interpolation to interpolate results from coarse to fine grid. This process is depicted in the following figure. | ||
<br/> | <br/> | ||
| − | [[Image:Multilevel_diagram.jpg| Multi-resolution Implementation | | + | [[Image:Multilevel_diagram.jpg| Multi-resolution Implementation | 700px | center]] |
| Line 39: | Line 39: | ||
| − | + | == Progress == | |
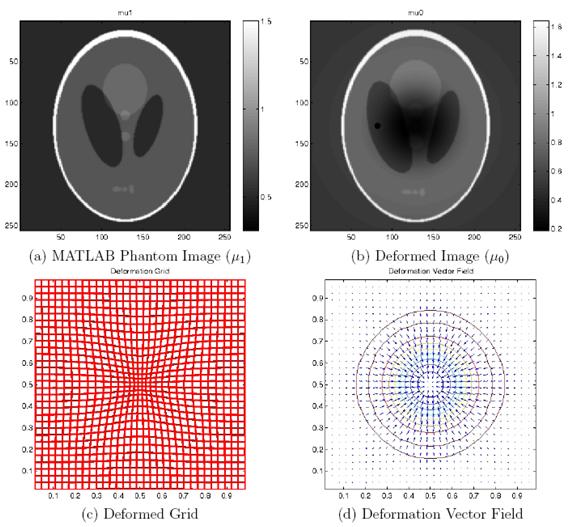
The algorithm was tested on a synthetic 3D dataset comprising of a sphere and deformed version of it. The deformation vector field for this experiment are shown below: | The algorithm was tested on a synthetic 3D dataset comprising of a sphere and deformed version of it. The deformation vector field for this experiment are shown below: | ||
| Line 53: | Line 53: | ||
| − | + | == Project Status == | |
* 2D Multi-resolution Registration using Optimal Mass Transport implemented. | * 2D Multi-resolution Registration using Optimal Mass Transport implemented. | ||
| Line 60: | Line 60: | ||
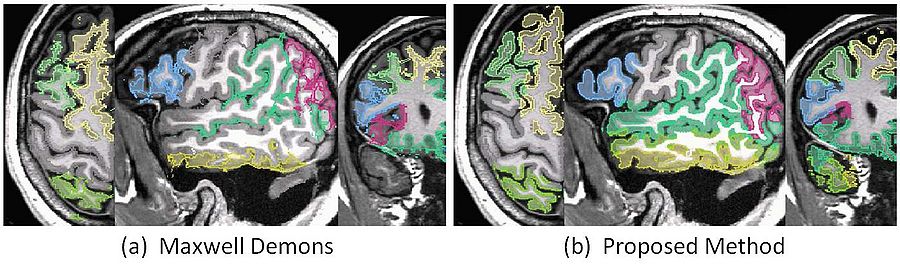
* 3D Registration of White Matter MRI data and white matter atlas implemented. The proposed new algorithm and the preliminary results are shown below: | * 3D Registration of White Matter MRI data and white matter atlas implemented. The proposed new algorithm and the preliminary results are shown below: | ||
| − | * [[Image:Wm_2_atlas_omt.jpg | Proposed Algorithm | | + | * [[Image:Wm_2_atlas_omt.jpg | Proposed Algorithm | 700px | center]] |
| + | * | ||
| + | * [[Image:Whitematter_tessalation.jpg | white matter to Atlas Registration Results | 900px | center]] | ||
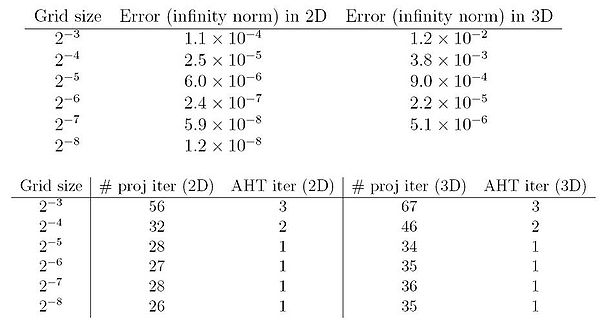
| − | * | + | * An Efficient Numerical Implementation of the OMT algorithm with explicit projections to the mass preserving constraint has been developed. The originally proposed method of integration of a time dependent PDE is replaced with a direct variational method. The projection step is computed using an Inexact Sequential Quadratic Programming (SQP) approach as shown below. The resulting KKT system is solved using a MINRES iteration and multigrid preconditioning. When using a consistent discretization approach the resulting algorithm is a stable second order method requiring few iterations to reach convergence as shown in the results below. |
| − | * | + | * [[Image:Inexact_SQP.jpg | Inexact SQP | 500px | center]] |
| − | * | + | |
| + | * [[Image:Synthetic_result1.jpg | Inexact SQP | 600px | center]] | ||
| + | |||
| + | * [[Image:Synthetic_result2.jpg | Inexact SQP | 600px | center]] | ||
| + | |||
| + | * Currently working on computation of the mass transport using OcTrees which can potentially result in an order of magnitude reduction in computational cost. | ||
= Key Investigators = | = Key Investigators = | ||
| Line 74: | Line 81: | ||
= Publications = | = Publications = | ||
| − | + | ''In Print'' | |
| − | + | * [http://www.na-mic.org/publications/pages/display?search=OptimalMassTransportRegistration&submit=Search&words=all&title=checked&keywords=checked&authors=checked&abstract=checked&sponsors=checked&searchbytag=checked| NA-MIC Publications Database on Optimal Mass Transport Registration] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ''In Press'' | |
| − | + | * Eldad Haber, Tauseef Rehman, and Allen Tannenbaum. An Efficient Numerical Method for the Solution of the L2 Optimal Mass Transfer Problem. In submission - SIAM Journal of Scientific Computing, 2009. | |
| − | + | * Tauseef Rehman, Eldad Haber, Gallagher Pryor, and Allen Tannenbaum. Fast Optimal Mass Transport for 2D Image Registration and Morphing. Accepted for - Elsevier Journal of Image and Vision Computing, 2009. | |
| − | |||
| − | |||
| − | |||
| + | Project Week Results: [[2008_Summer_Project_Week:DWIRegistrationOMT|June 2008]] | ||
[[Category:Registration]] [[Category:MRI]] | [[Category:Registration]] [[Category:MRI]] | ||
Latest revision as of 00:58, 16 November 2013
Home < Projects:OptimalMassTransportRegistrationBack to Stony Brook University Algorithms
Optimal Mass Transport
The aim of this project to provide a computationaly efficient non-rigid/elastic image registration algorithm based on the Optimal Mass Transport theory. We use the Monge-Kantorovich formulation of the Optimal Mass Transport problem and implement the solution proposed by Haker et al. using multi-resolution and multigrid techniques to speed up the convergence. We also leverage the computation power of general purpose graphics processing units available on standard desktop computing machines to exploit the inherent parallelism in our algorithm.
Description
The Optimal Mass Transport problem was first formulated by a Frech engineer Gasper Monge in 1781, and was given a modern formulation in the work of Kantorovich and, therefore, is now known as the Monge-Kantorovich problem. We extend the work by Haker et al. who compute the optimal warp from a first order partial differential equation, an improvement over earlier proposed higher order methods and those based on linear programming. We implement the algorithm using a coarse-to-fine strategy resulting in phenomenol improvement in convergence. The algorithm also involves inverting the Laplacian in each iteration, which we perform using multigrid methods for even faster per iteration computation times. This method has a number of distinguishing characteristics:
- It is a parameter free method.
- It utillizes all of the grayscale data in both images.
- It is symmetrical; the optimal mapping from image A to image B is the inverse of the optimal mapping from B to A.
- No landmarks need to be specified.
- The minimizer of the functional involved is unique; there are no local minimizers.
- The algorithm is designed to take into account changes in densities that result from changes in area or volume.
Algorithm
The flowchart of the algorithm is shown in the following figure.
Multi-resolution Approach
Performing image registration using a multi-resolution approach is widely used to improve speed, accuracy and robustness. Registration is first performed at a coarse scale. The spatial mapping determined at coarse scale is then used to initialize registration at the next finer scale. This process is repeated until it reaches the finest scale. Our coarse-to-fine hierarchy comprises of three levels and we use bi-cubic interpolation to interpolate results from coarse to fine grid. This process is depicted in the following figure.
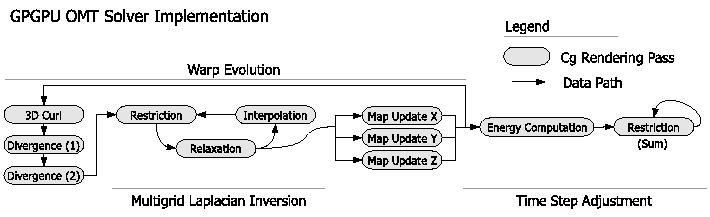
The following figure shows the outline of processing for the OMT solver conducted on the GPU. Processing occurs in two major phases: evolution of the map from
source to target volumes and time step adjustment. Each gray rectangle represents one Cg kernel executed on the GPU. Arrows indicate the
flow of data volumes through the Cg kernels. The entire process in the figure, above is repeated left to right until convergence.
Progress
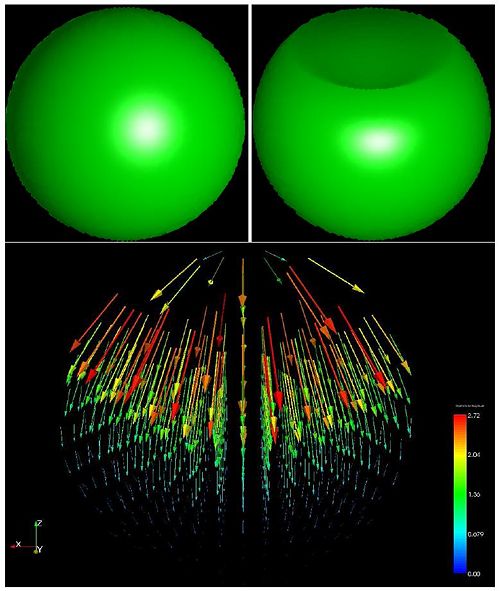
The algorithm was tested on a synthetic 3D dataset comprising of a sphere and deformed version of it. The deformation vector field for this experiment are shown below:
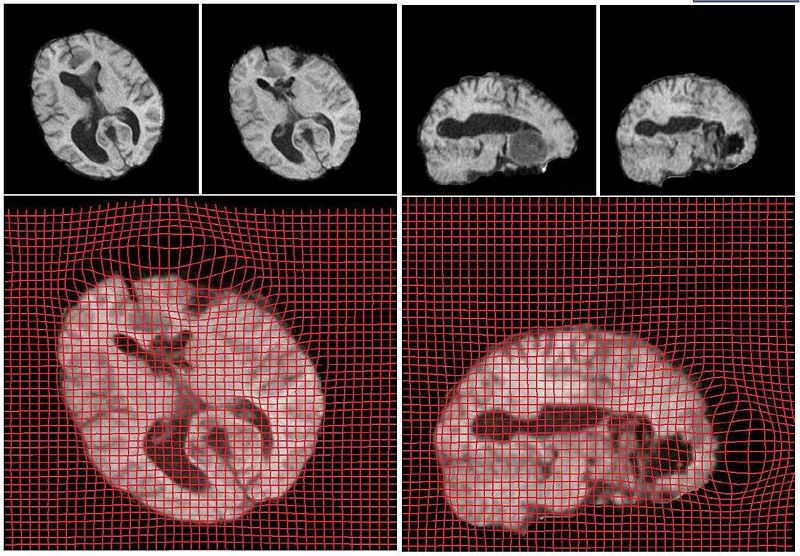
Below we show the results from registration of two 3D brain MRI datasets. The first data set was pre-operative while the second data set was acquired during surgery (craniotomy). Both were resampled to 256*256*256 for uniform voxel size and the skull was removed. We show the results on an axial and a coronal slice of the 3D brain volumes. The sag and compression areas can easily be seen in the deformed grid shown below. The reults shown are after 3600 iterations, requiring less than 15 minutes of computation time (Dual Xeon 1.6GHz + nVidia GeForce 8800 GX GPU. The optimal computation time was found to occur for a grid size of 128*128*128 where about 1000 iterations execute in less than 15 seconds. This is due to the memory limitations on the graphics card used. The results on an axial and coronal slice are shown below:
Project Status
- 2D Multi-resolution Registration using Optimal Mass Transport implemented.
- 3D Multi-resolution Registration using Optimal Mass Transport of Brain sag datasets implemented.
- 3D Registration of White Matter MRI data and white matter atlas implemented. The proposed new algorithm and the preliminary results are shown below:
- An Efficient Numerical Implementation of the OMT algorithm with explicit projections to the mass preserving constraint has been developed. The originally proposed method of integration of a time dependent PDE is replaced with a direct variational method. The projection step is computed using an Inexact Sequential Quadratic Programming (SQP) approach as shown below. The resulting KKT system is solved using a MINRES iteration and multigrid preconditioning. When using a consistent discretization approach the resulting algorithm is a stable second order method requiring few iterations to reach convergence as shown in the results below.
- Currently working on computation of the mass transport using OcTrees which can potentially result in an order of magnitude reduction in computational cost.
Key Investigators
- Georgia Tech: Tauseef ur Rehman, Ivan Kolesov, Gallagher Pryor, Eldad Haber, Allen Tannenbaum
- BWH: Sylvain Bouix, Yogesh Rathi, Ron Kikinis
Publications
In Print
In Press
- Eldad Haber, Tauseef Rehman, and Allen Tannenbaum. An Efficient Numerical Method for the Solution of the L2 Optimal Mass Transfer Problem. In submission - SIAM Journal of Scientific Computing, 2009.
- Tauseef Rehman, Eldad Haber, Gallagher Pryor, and Allen Tannenbaum. Fast Optimal Mass Transport for 2D Image Registration and Morphing. Accepted for - Elsevier Journal of Image and Vision Computing, 2009.
Project Week Results: June 2008