Projects:MultimodalAtlas
Back to NA-MIC Collaborations, MIT Algorithms, Harvard DBP2
Today, computational anatomy studies are mainly hypothesis-driven, aiming to identify and characterize structural or functional differences between, for instance a group of patients with a specific disorder and control subjects. This type of approach has two premises: clinical classification of the subjects and spatial correspondence across the images. In practice, achieving either can be challenging. First, the complex spectrum of symptoms of neuro-degenerative disorders like schizophrenia and overlapping symptoms across different types of dementia like Alzheimer's disease, delirium and depression make a diagnosis based on standardized clinical tests like the mental status examination difficult. Second, across-subject correspondence in the images is a particularly hard problem that requires different approaches in various contexts. A popular technique is to normalize all subjects into a standard space, such as the Talairach space, by registering each image with a single, universal template image that represents an average brain. However, the quality of such an approach is limited by the accuracy with which the universal template represents the population in the study.
With the increasing availability of medical images, data-driven algorithms offer the ability to probe a population and potentially discover sub-groups that may differ in unexpected ways. In this paper, we propose and demonstrate an efficient probabilistic clustering algorithm, called iCluster, that:
- computes a small number of templates that summarize a given population of images,
- simultaneously co-registers all the images using a nonlinear transformation model,
- assigns each input image to a template.
The templates are guaranteed to live in an affine-normalized space, i.e., they are spatially aligned with respect to an affine transformation model.
Description
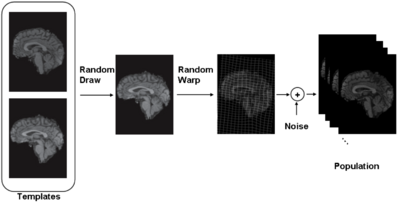
iCluster is derived from a simple generative model. We assume that there are a fixed and known number of template images. Then the process that generates an observed image is as follows: a template is randomly drawn – note that the probability that governs this process doesn’t have to be uniform. Next, the chosen template is warped with a random transformation and i.i.d Gaussian noise is added to this warped image to generate an observed image. This process is repeated multiple times to generate a collection of images.
We formulate the problem as a maximum likelihood solution. We employ a Generalized Maximum Likelihood (GEM) algorithm to solve the problem. The GEM algorithm is derived using Jensen's inequality and has three steps:
- E-step: Given the estimates for the template images, template prior probabilities and noise variance image estimates from the previous iteration, the algorithm updates the memberships of each image as the posterior probability of an image being generated from a particular template.
- T-step: Given the membership estimates from the previous E-step, the algorithm updates the template image, template prior and noise variance estimates using closed-form expressions.
- R-step: Given the membership, template, template prior and noise variance estimates from the pervious iterations, the algorithm updates the warps for each image. This step is a collection of pairwise registration instances, where each image is aligned with an effective template image. The effective template image is a weighted average of the current individual templates, where the weights are current memberships.
The resulting algorithm is fast and efficient: each iteration's time and memory requirements are linear in the number of voxels, input images and templates. We employ a stochastic subsampling strategy in each one of the E, T and R steps. A random subsample of voxels (typically less than 1% of the total voxels) are used for the computations. In the R-step, we employ a B-spline nonlinear transformation model and the optimization is done using gradient-descent. During this optimization, the gradients are normalized so that each cluster (i.e. the images assigned to the same template image) are subject to an average of zero deformation. This is an extension of the "anchoring" strategy used in groupwise registration algorithms. This is usually done by subtracting the average gradient from the individual gradients.
Results
We present two experiments. The first one demonstrates the use of iCluster for building a multi-template atlas in a segmentation application. In the second experiment, we employ iCluster to compute multiple templates of a large data set that contains 416 brain MRI. Our results show that these templates correspond to different age groups. We find the correlation between the image-based clustering, and demographic and clinical characteristics particularly intriguing, given the fact that iCluster did not employ the latter information.
Experiment 1: Segmentation Label Alignment
In this experiment, we used a data set of 50 whole brain MR brain images (of size 256x256x124 and voxel dimensions 0.9375x0.9375x1.5 mm) that contained 16 patients with first episode schizophrenia (SZ), 17 patients with first-episode affective disorder (AFF) and 17 healthy subjects (CON). First episode patients are relatively free of chronicity-related confounds such as the long-term effects of medication, thus any structural differences between the three groups are subtle, local and difficult to identify in individual scans.
The 50 MR images also contained manual labels of certain medial temporal lobe structures: the superior temporal gyrus (STG), hippocampus (HIPP), amygdala (AMY) and parahippocampal gyrus (PHG). We used these manual labels to explore label alignment across subjects under different groupings: on the whole data set, on random partitionings of the data set into two subsets of equal size, on the clinical grouping, and on the image-based clustering as determined by iCluster.
'Software'
The algorithm is currently implemented in the Insight ToolKit (ITK) and will be made publicly available. We also plan to integrate it into Slicer.
Key Investigators
MIT Algorithms: Mert R. Sabuncu and Polina Golland
Harvard DBP 2: M.E. Shenton, M. Kubicki and S. Bouix
Publications
In Print