Projects:WaveletShrinkage

Back to NA-MIC Collaborations, Georgia Tech Algorithms

Description

Shape analysis has become a topic of interest in medical imaging since local variations of a shape could carry relevant information about a disease that may affect only a portion of an organ. We developed a novel wavelet-based denoising and compression statistical model for 3D shapes.

Method

Shapes are encoded using spherical wavelets that allow for a multiscale shape representation by decomposing the data both in scale and space using a multiresolution mesh (See Nain et al. MICCAI 2005). This representation also allows for efficient compression by discarding wavelet coefficients with low values that correspond to irrelevant shape information and high frequency coefficients that represent noisy artifacts. This process is called hard wavelet shrinkage and has been widely researched for traditional types of wavelets, but not much explored for second generation wavelets.

In the wavelet domain, shapes are modeled as a sum of a vector of signal coefficients with noisy coefficients.

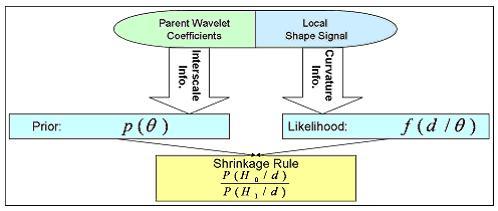
We develop a non-linear wavelet shrinkage model based on a data-driven Bayesian framework that will adaptively threshold wavelet coefficients in order to keep the signal part of our shapes. Our threshold rule locally takes into account shape curvature and interscale dependencies between neighboring wavelet coefficients. Interscale dependencies enable us to use the correlation that exists between levels of decomposition by looking at coefficient’s parents. A coefficient will be very likely to be shrunk if the local curvature is low and if its parents are low-valued.

Our Bayesian framework incorporates that information as follows:

Key Investigators

• Georgia Tech: Xavier Le Faucheur, Allen Tannenbaum, Delphine Nain

Publications

In press

• Bayesian Spherical Wavelet Shrinkage:Applications to shape analysis, X. Le Faucheur, B. Vidakovic, A. Tannenbaum, Proc. of SPIE Optics East, 2007.