Projects:WaveletShrinkage
Back to NA-MIC Collaborations, Stony Brook University Algorithms
Wavelet Shrinkage for Shape Analysis
Description
Shape analysis has become a topic of interest in medical imaging since local variations of a shape could carry relevant information about a disease that may affect only a portion of an organ. We developed a novel wavelet-based denoising and compression statistical model for 3D shapes.
Method
Shapes are encoded using spherical wavelets that allow for a multiscale shape representation by decomposing the data both in scale and space using a multiresolution mesh (See Nain et al. MICCAI 2005). This representation also allows for efficient compression by discarding wavelet coefficients with low values that correspond to irrelevant shape information and high frequency coefficients that represent noisy artifacts. This process is called hard wavelet shrinkage and has been widely researched for traditional types of wavelets, but not much explored for second generation wavelets.
In the wavelet domain, we model a shape as a vector of coefficients, consisting in the sum of signal part coefficients and coefficients considered as noise:
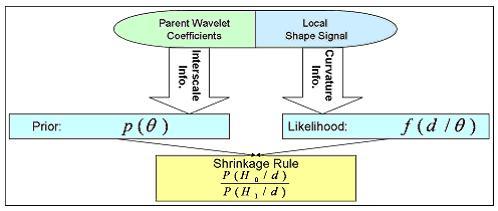
We develop a non-linear statistical wavelet shrinkage model based on a data-driven framework that will adaptively threshold wavelet coefficients in order to accurately estimate the noiseless part of the shape signal. In fact, the proposed selection model in the wavelet domain is based on a Bayesian hypotheses testing: a given wavelet coefficient will either be kept (null hypothesis rejected) or get shrunk to zero (null hypothesis non rejected). Our threshold rule locally takes into account shape curvature and interscale dependencies between neighboring wavelet coefficients. Interscale dependencies enable us to take advantage of the correlation that exists between levels of decomposition by looking at coefficients' parents, and curvature terms will help adjust strength of shrinkage by locally looking at the coarse shape variations. A coefficient will be very likely to be shrunk if local curvature is low and if its parents are low-valued.
Our Bayesian framework incorporates that information as follows:
Validation
Our validation shows how this new wavelet shrinkage framework outperforms classical compression and denoising methods for shape representation. We apply our method to the denoising of the left hippocampus and caudate nucleus from MRI brain data. In the following figures, we compare our denoising results to those obtained with universal thresholding (Donoho, 1995) and to the method that we previously developed (SPIE Optics East, 2007), which was based on inter- and intra-scale dependent shrinkage.
Shrinkage is applied to left hippocampus shapes for denoising: (a) original shape, (b) noisy shape, (c) results with traditional thresholding, (d) inter-/intra-scale and (e) proposed Bayesian method (in (c),(d),(e) color is normalized reconstruction error at each vertex (in % of the shape bounding box) from blue (lowest) to red)
We actually are able to remove more than 90% of the coefficients from the fine levels while recovering an accurate estimation of the original shape. Our data-driven Bayesian framework allows us to obtain a spatially consistent model for wavelet shrinkage as it preserves intrinsic features of the shape and keeps the smoothing process under control.
Key Investigators
- Georgia Tech: Xavier Le Faucheur, Allen Tannenbaum, Delphine Nain
Publications
In print
NA-MIC Publications Database on Wavelet Shrinkage for Shape Analysis