Projects/Diffusion/Contrasting Tractography Measures
Contrasting Tractography Methods Conference - Oct 1-2, 2007, Santa Fe
Overview
| Site | Streamline Tractography Algorithm | Input | Volumetric Output | Geometric Output | Other Information |
| UNC | Streamline (Fiber Viewer) | DTI | None | Tracts | see here |
| BWH | Streamline (Slicer) | DWI | None | Tracts | see here |
| JHU | Streamline (DTI Studio) | DWI | None | Tracts | see here |
| Iowa | Streamline (GTract) | DTI | None | Tracts | see here |
| Site | Volumetric Connectivity Filter Algorithm | Input | Volumetric Output | Geometric Output | Other Information |
| GaTech | Geodesic Active Contours (Finsler/Riemannian) | DWI or DTI | Labelmap per bundle | Optimal path | see here |
| BWH | Stochastic | DWI | Probability Map | None | see here |
| Utah | Volumetric Connectivity (Riemannian) | DWI or DTI | Tract label map | Isosurface of tract | see here |
| UCLA | Fluid Mechanics Tractography | ||||
| MGH | PROBTRACK | DWI | Probability Map | Tracts | will not be presented |
UNC
Overview of UNC Tractography Methods
The UNC tractography measure methodology produces fiber bundles using a standard streamline tractography algorithm FiberTracking. The fiber bundles are attributed with tensor data at each point along the bundle. The user uses clustering and manual editing tools in FiberViewer to identify the fiber bundle and remove outliers. The user identifies an origin on the fiber bundle and computes statistics of the bundle as a function of arc-length along the bundle.
- Inputs
- DWI or DTI
- ROI for seed regions for tractography
- Outputs
- Fiber bundle tracts viewable in FiberViewer or Slicer3
- Summary statistics of fiber bundle as function of arc length (text file)
Iowa
The University of Iowa tractography program GTRACT is based on a modified streamlines algorithm. The advantage of this algorithm is that it helps to resolve fibers in regions where there are crossing or fanning fibers. We have also instrumented a fast marching based algorithm into GTRACT that we are currently evaluating. These algorithms require a seed region as input and will generate a VTK file representing the fiber tracts. Data associated with anisotropy, curvature or cost of the tract can be included as point data associated with the fiber tract. Tools are also available for computing the distance between fiber tracts.
- Inputs
- DWI or DTI data (DICOM or other ITK supported format)
- Parameters defining the diffusion directions
- Binary image representing the regions of interest for seeds
- Outputs
- Tensor image
- ADC and anisotropy images as defined by the user
- Fiber tracts in VTK format
GATech
Geodesic Active Contours for Fiber Tractography and Fiber Bundle Segmentation
These algorithms find the optimal path (i.e. "the anchor tract") connecting two ROIs, which is equivalent to finding a geodesic on a manifold (which may be any Finsler manifold, such as the Riemannian manifold). Then, the associated fiber bundles is segmented from the data via a region-based flow adapted for DW-MRI direction-dependent data.
- Inputs
- DWI or DTI
- ROI for seed regions (i.e. the endpoints of the fiber bundle, which most likely correspond to the associated gray matter regions)
- Outputs
- VTK files of the anchor tracts
- VTK files of the volumetric fiber bundle
- Summary statistics of fiber bundle as function of arc length (text file)
Note, I've put this together which may have some educational and/or thought provoking value. It is certainly biased towards the ideas entertained at Georgia Tech over the past few years and could be greatly extended/enhanced with more input from others in the community. Check it out here: DW-MRI Musings.
BWH
Stochastic Tractography
Stochastic Tractography is a Bayesian approach to estimating nerve fiber tracts from DWMRI (Diffusion Weighted Magnetic Imaging) images. The Bayesian framework provides a measure of confidence regarding the estimated tracts. This measure of confidence allows the algorithm to generate tracts which pass through regions with uncertain fiber directions, revealing more details about structural connectivity than non-Bayesian tractography algorithm.
- Inputs
- DWI and associated parameters (b-values, gradient directions)
- Posterior White Matter probability map
- Outputs
- Brain Connectivity Map
- Tract-Averaged FA Distribution
- Tract Length Distribution
UTAH
This is a PDE-based approach to white matter connectivity from DTI that is founded on the principal of minimal paths through the tensor volume. Our method computes a volumetric representation of a white matter tract given two endpoint regions. We have also developed statistical methods for quantifying the full tensor data along these pathways, which should be useful in clinical studies using DT-MRI.
- Input
- DWI or DTI
- ROIs of tract endpoints
- Output
- Labelmap of tract
- Parameterization along tract
- Regression of tensor data along tract (tensors, FA, MD, etc)
BWH
The DT-MRI module of Slicer uses a streamline tractography algorithm with a mutilple-ROI approach (AND and NOT operators).
- Inputs
- DWI or DTI data
- ROI
- Outputs
- Fiber tracts in VTK format
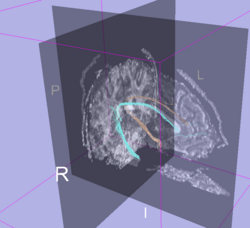
Example: Cingulum bundle generated from the validation data ROIs.
BWH
The single-subject clustering uses trajectory similarity to create bundles. The atlas clustering identifies bundles that have been learned from a group DTI dataset.
- Inputs
- DWI or DTI data
- Mask defining brain region (to avoid seeding tracts outside the brain)
- From the above, whole brain streamline tractography is generated
- Desired number of bundles/clusters OR existing cluster atlas.
- Outputs
- Fiber bundle clusters (in vtk format)
MGH
The goal of the POIStats (Path-of-Interest Statistics) algorithm is to calculate the highest probability path between two user-defined seed regions from DTI. The best path is determined by minimizing the energy of the entire path through randomization of the position of the control points of a spline curve drawn through the data and of the position of the endpoints.
- Input
- DTI
- ROIs of tract endpoints and/or intermediate points
- Output
- Volume label map of tracts
- Probability optimal path goes through voxels
- Coordinates of optimal path
Return to ContrastingTractography Project Page