Difference between revisions of "Algorithm:Utah"
m (Fix MediaWiki table formatting issue discovered while converting to GitHub Flavored Markdown using pandoc (via https://github.com/outofcontrol/mediawiki-to-gfm)) Tag: 2017 source edit |
|||
| (93 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
Back to [[Algorithm:Main|NA-MIC Algorithms]] | Back to [[Algorithm:Main|NA-MIC Algorithms]] | ||
__NOTOC__ | __NOTOC__ | ||
| − | = Overview of Utah Algorithms = | + | = Overview of Utah Algorithms (PI: Ross Whitaker) = |
| − | + | We are developing new methods in the areas of statistical shape analysis, MRI tissue segmentation, and diffusion tensor image processing and analysis. We are building shape analysis tools that can generate efficient statistical models appropriate for analyzing anatomical shape differences in the brain. We are developing a wide range of tools for diffusion tensor imaging, that span the entire pipeline from image processing to automatic white matter tract extraction to statistical testing of clinical hypotheses. | |
= Utah Projects = | = Utah Projects = | ||
| − | {| | + | {| cellpadding="10" style="text-align:left;" |
| − | | style="width: | + | |
| − | | style="width: | + | |
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:sgerber_brainmanifold_oasis_manifold.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:BrainManifold|Brain Manifold Learning]] == | ||
| + | |||
| + | This work is concerned with modeling high dimensional spaces, such as the space of brain images. Common approach for representing populations are template or clustering based approaches. In this project we develop a data driven method to learn a manifold representation from a set of brain images. The presented approach is described and evaluated in the setting of brain MRI but generalizes to other application domains. | ||
| + | |||
| + | S Gerber, T Tasdizen, S Joshi, R Whitaker, On the Manifold Structure of the Space of Brain Images, MICCAI 2009. | ||
| + | |||
| + | S Gerber, T Tasdizen, R Whitaker, Dimensionality Reduction and Principal Surfaces via Kernel Map, ICCV 2009. | ||
| + | |||
| + | S. Gerber, T. Tasdizen, P.T. Fletcher, S. Joshi, R. Whitaker, Manifold Modeling for Brain Population Analysis, Medical Image Anal, 3, 2010. | ||
| + | |||
| + | |||
| + | |- | ||
| + | | style="width:15%" | [[Image:EPI.png|200px]] | ||
| + | | style="width:85%" | | ||
| + | |||
| + | == [[Projects:EPIDistortionCorrection| Correction for Geometric Distortion in Echo Planar Images]] == | ||
| + | |||
| + | We have developed a variational image-based approach to correct the susceptibility artifacts in the alignment of diffusion weighted and structural MRI.The correction is formulated as an optimization of a penalty that captures the intensity difference between the jacobian corrected EPI baseline images and a corresponding T2-weighted structural image. | ||
| + | |||
| + | <font color="red"></font> R Tao, P T Fletcher, S Gerber, R Whitaker, A Variational Image-Based Approach to the Correction of Susceptibility Artifacts | ||
| + | in the Alignment of Diffusion Weighted and Structural MRI, IPMI 2009. | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:pipeline.png|150px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:StructuralAndDWIPipeline| A Framework for Joint Analysis of Structural and Diffusion MRI]] == | ||
| + | |||
| + | This framework addresses the simultaneous alignment and filtering of DWI images to correct eddy current artifacts and the subsequent alignment of those images to structural, T1 MRI to correct for susceptibility artifacts, and this paper demonstrates the importance of performing these corrections. It also shows how a T1-based, group specific atlas can be used to generate grey-matter regions of interest that can drive subsequent connectivity analyses. The result is a system that can be combined with a variety of tools for MRI analysis for tissue classification, morphometry, and cortical parcellation. | ||
| + | |||
| + | <font color="red"></font> Ran Tao, P. Thomas Fletcher, Ross T. Whitaker, in MICCAI 2008 on Computational Diffusion MRI. | ||
| + | |||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:Sulcaldepth.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:CorticalCorrespondenceWithParticleSystem|Cortical Correspondence using Particle System]] == | ||
| + | |||
| + | In this project, we want to compute cortical correspondence on populations, using various features such as cortical structure, DTI connectivity, vascular structure, and functional data (fMRI). This presents a challenge because of the highly convoluted surface of the cortex, as well as because of the different properties of the data features we want to incorporate together. [[Projects:CorticalCorrespondenceWithParticleSystem|More...]] | ||
| + | |||
| + | <font color="red"></font> Oguz I, Niethammer M, Cates J, Whitaker R, Fletcher T, Vachet C, Styner M. “Cortical Correspondence with Probabilistic Fiber Connectivity”. Proc. Information Processing in Medical Imaging, 2009. | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:CatesNamicFigure3.png|200px]] | ||
| + | | | | ||
== [[Projects:ParticlesForShapesAndComplexes|Adaptive, Particle-Based Sampling for Shapes and Complexes]] == | == [[Projects:ParticlesForShapesAndComplexes|Adaptive, Particle-Based Sampling for Shapes and Complexes]] == | ||
| − | + | This research is a new method for constructing compact statistical point-based models of ensembles of similar shapes that does not rely on any specific surface parameterization. The method requires very little preprocessing or parameter tuning, and is applicable to a wider range of problems than existing methods, including nonmanifold surfaces and objects of arbitrary topology. [[Projects:ParticlesForShapesAndComplexes|More...]] | |
| + | |||
| + | <font color="red"></font> Particle-Based Shape Analysis of Multi-object Complexes. Cates J., Fletcher P.T., Styner M., Hazlett H.C., Whitaker R. Int Conf Med Image Comput Comput Assist Interv. 2008;11(Pt 1):477-485. | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:UNCShape_OverviewAnalysis_MICCAI06.gif|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:ShapeAnalysisFrameworkUsingSPHARMPDM|Shape Analysis Framework using SPHARM-PDM]] == | ||
| + | |||
| + | The UNC shape analysis is based on an analysis framework of objects with spherical topology, described mainly by sampled spherical harmonics SPHARM-PDM. The input of the shape analysis framework is a set of binary segmentations of a single brain structure, such as the hippocampus or caudate. These segmentations are converted into a shape description (SPHARM) with correspondence and analyzed via Hotelling T^2 two sample metric. [[Projects:ShapeAnalysisFrameworkUsingSPHARMPDM|More...]] | ||
| + | |||
| + | <font color="red"></font> Zhao Z., Taylor W., Styner M., Steffens D., Krishnan R., Macfall J. , Hippocampus shape analysis and late-life depression. PLoS ONE. 2008 Mar 19;3(3):e1837. | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:HeadRegressionResult.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:ShapeRegression|Particle Based Shape Regression]] == | ||
| + | |||
| + | Shape regression promises to be an important tool to study the relationship between anatomy and underlying clinical or biological parameters, such as age. We propose a new method to building shape models that incorporates regression analysis in the process of optimizing correspondences on a set of open surfaces. The method is applied to provide new results on clinical MRI data related to early development of the human head. | ||
| + | |||
| + | M Datar, J Cates, P T Fletcher, S Gouttard, G Gerig, R Whitaker, Particle Based Shape Regression of Open Surfaces with Applications to Developmental Neuroimaging, MICCAI 2009. | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:NonRegularSurfCorres.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:NonRegularSurfCorres|Geometric Correspondence for Nonregular Surfaces]] == | ||
| + | |||
| + | To resolve the challenges posed by highly nonregular surfaces, we have proposed an efficient method which incorporates Geodesic distances and an entropy based on surface normals to improve correspondences. | ||
| + | |||
| + | M Datar, Y Gur, B Paniagua, M Styner, R Whitaker,Geometric Correspondence for Ensembles of Nonregular Shapes, MICCAI 2011. | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:MixedEffectsShape.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:MixedEffectsShape|Mixed-Effects Shape Models for Longitudinal Analysis]] == | ||
| + | |||
| + | Longitudinal shape changes in anatomy are characterized using a new method that combines point correspondences across shapes with the statistical modeling of individual and population trends via the linear mixed-effects model. This method helps us examine and contrast population trends with individual growth trajectories. | ||
| + | |||
| + | <font color="red">'''New: '''</font> M Datar, P Muralidharan, A Kumar, S Gouttard, J Piven, G Gerig, RT Whitaker, PT Fletcher,Mixed-Effects Shape Models for Estimating Longitudinal Changes in Anatomy, STIA 2012 | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:CamFAIAnalysis.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == Statistical Shape Analysis of Cam-FAI == | ||
| + | |||
| + | Cam femoroacetabular impingement (FAI) is characterized by a malformed femoral head that may lead to early hip osteoarthritis. Radiographic measurements are used to diagnose cam FAI and often assume the femur shape to be spherical. Statistical shape modeling (SSM) can be used to compare complex 3D morphology without the need to assume ideal geometry and quantify morphologic differences between control and FAI femurs. | ||
| + | |||
| + | <font color="red">'''New: '''</font> MD Harris, M Datar, E Jurrus, CL Peters, RT Whitaker, AE Anderson, [http://www.cs.utah.edu/~manasi/pubs/CM165P.pdf|Statistical Shape Modeling of CAM-type Femoroacetabular Impingement], CMBBE 2012 | ||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:MiceMOAnalysis.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == Understanding Short Bone Phenotype in Multiple Osteochondromas == | ||
| + | |||
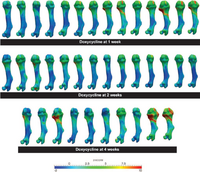
| + | Novel statistical methods were developed to study the 'steal phenomenon' caused by multiple osteochondromas in mouse models. Bone lengths and volumes were compared. Metaphyseal volume deviations from normal, as a measure of osteochondroma volumetric growth, were correlated with length deviations. | ||
| − | <font color="red">'''New: '''</font> | + | <font color="red">'''New: '''</font> KB Jones, M Datar, S Ravichandran, H Jin, E Jurrus, RT Whitaker, MR Capecchi, Toward an Understanding of the Short Bone Phenotype Associated with Multiple Osteochondromas, JOR 2012 (to appear) |
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:FiberTracts-angle.jpg|200px]] |
| | | | | | ||
== [[Projects:DTIVolumetricWhiteMatterConnectivity|DTI Volumetric White Matter Connectivity]] == | == [[Projects:DTIVolumetricWhiteMatterConnectivity|DTI Volumetric White Matter Connectivity]] == | ||
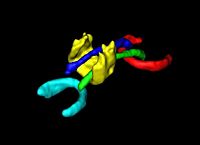
| − | + | We have developed a PDE-based approach to white matter connectivity from DTI that is founded on the principal of minimal paths through the tensor volume. Our method computes a volumetric representation of a white matter tract given two endpoint regions. We have also developed statistical methods for quantifying the full tensor data along these pathways, which should be useful in clinical studies using DT-MRI. [[Projects:DTIVolumetricWhiteMatterConnectivity|More...]] | |
| + | |||
| + | |- | ||
| + | | style="width:15%" | [[Image:DTIFiltering.jpg|200px]] | ||
| + | | style="width:85%" | | ||
| + | |||
| + | == [[Projects:DTIProcessingTools|DTI Processing and Statistics Tools]] == | ||
| − | + | We implement the diffusion weighted image (DWI) registration model from the paper of G.K.Rohde et al. Patient head motion and eddy currents distortion cause artifacts in maps of diffusion parameters computer from DWI. This model corrects these two distortions at the same time including brightness correction. | |
|- | |- | ||
| − | | | [[Image: | + | | | [[Image:Brain-seg-utah.png|200px]] |
| − | | | | + | | | |
== [[Projects:TissueClassificationWithNeighborhoodStatistics| Tissue Classification with Neighborhood Statistics]] == | == [[Projects:TissueClassificationWithNeighborhoodStatistics| Tissue Classification with Neighborhood Statistics]] == | ||
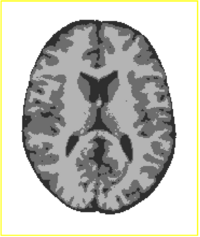
| − | + | We have implemented an MRI tissue classification algorithm based on unsupervised non-parametric density estimation of tissue intensity classes. | |
| + | [[Projects:TissueClassificationWithNeighborhoodStatistics|More...]] | ||
| + | |||
| + | |||
| + | |- | ||
| + | |||
| + | | | [[Image:combined_50_seg_labeled.png|200px]] | ||
| + | | | | ||
| + | |||
| + | == [[Projects:AtlasBasedBrainSegmentation| Atlas-Based Brain Segmentation]] == | ||
| + | |||
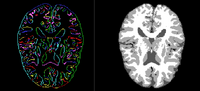
| + | We have implemented an Multi-Atlases based brain MRI tissue segmentation method. This method using a fast,shape-based hierarchical matching approach to find the kNNs for a target brain in a brain dataset with known segmentations/labels, and then fuse the labels of the kNNs instead of the labels of all images in the dataset, which can give an accurate atlas for the target. | ||
| − | <font color="red"> | + | <font color="red"></font> P. Zhu, S.P. Awate, S. Gerber, R. Whitaker. Fast Shape-Based Nearest-Neighbor Search for Brain MRIs Using Hierarchical Feature Matching, MICCAI 2011. |
|} | |} | ||
Latest revision as of 06:22, 11 April 2023
Home < Algorithm:UtahBack to NA-MIC Algorithms
Overview of Utah Algorithms (PI: Ross Whitaker)
We are developing new methods in the areas of statistical shape analysis, MRI tissue segmentation, and diffusion tensor image processing and analysis. We are building shape analysis tools that can generate efficient statistical models appropriate for analyzing anatomical shape differences in the brain. We are developing a wide range of tools for diffusion tensor imaging, that span the entire pipeline from image processing to automatic white matter tract extraction to statistical testing of clinical hypotheses.
Utah Projects
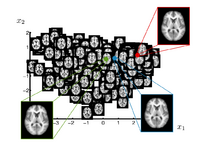
|
Brain Manifold LearningThis work is concerned with modeling high dimensional spaces, such as the space of brain images. Common approach for representing populations are template or clustering based approaches. In this project we develop a data driven method to learn a manifold representation from a set of brain images. The presented approach is described and evaluated in the setting of brain MRI but generalizes to other application domains. S Gerber, T Tasdizen, S Joshi, R Whitaker, On the Manifold Structure of the Space of Brain Images, MICCAI 2009. S Gerber, T Tasdizen, R Whitaker, Dimensionality Reduction and Principal Surfaces via Kernel Map, ICCV 2009. S. Gerber, T. Tasdizen, P.T. Fletcher, S. Joshi, R. Whitaker, Manifold Modeling for Brain Population Analysis, Medical Image Anal, 3, 2010.
|
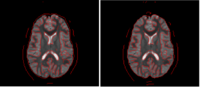
|
Correction for Geometric Distortion in Echo Planar ImagesWe have developed a variational image-based approach to correct the susceptibility artifacts in the alignment of diffusion weighted and structural MRI.The correction is formulated as an optimization of a penalty that captures the intensity difference between the jacobian corrected EPI baseline images and a corresponding T2-weighted structural image. R Tao, P T Fletcher, S Gerber, R Whitaker, A Variational Image-Based Approach to the Correction of Susceptibility Artifacts in the Alignment of Diffusion Weighted and Structural MRI, IPMI 2009. |
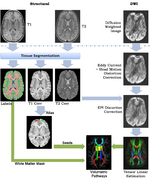
|
A Framework for Joint Analysis of Structural and Diffusion MRIThis framework addresses the simultaneous alignment and filtering of DWI images to correct eddy current artifacts and the subsequent alignment of those images to structural, T1 MRI to correct for susceptibility artifacts, and this paper demonstrates the importance of performing these corrections. It also shows how a T1-based, group specific atlas can be used to generate grey-matter regions of interest that can drive subsequent connectivity analyses. The result is a system that can be combined with a variety of tools for MRI analysis for tissue classification, morphometry, and cortical parcellation. Ran Tao, P. Thomas Fletcher, Ross T. Whitaker, in MICCAI 2008 on Computational Diffusion MRI.
|
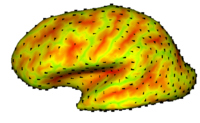
|
Cortical Correspondence using Particle SystemIn this project, we want to compute cortical correspondence on populations, using various features such as cortical structure, DTI connectivity, vascular structure, and functional data (fMRI). This presents a challenge because of the highly convoluted surface of the cortex, as well as because of the different properties of the data features we want to incorporate together. More... Oguz I, Niethammer M, Cates J, Whitaker R, Fletcher T, Vachet C, Styner M. “Cortical Correspondence with Probabilistic Fiber Connectivity”. Proc. Information Processing in Medical Imaging, 2009. |
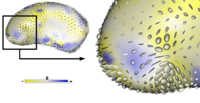
|
Adaptive, Particle-Based Sampling for Shapes and ComplexesThis research is a new method for constructing compact statistical point-based models of ensembles of similar shapes that does not rely on any specific surface parameterization. The method requires very little preprocessing or parameter tuning, and is applicable to a wider range of problems than existing methods, including nonmanifold surfaces and objects of arbitrary topology. More... Particle-Based Shape Analysis of Multi-object Complexes. Cates J., Fletcher P.T., Styner M., Hazlett H.C., Whitaker R. Int Conf Med Image Comput Comput Assist Interv. 2008;11(Pt 1):477-485. |

|
Shape Analysis Framework using SPHARM-PDMThe UNC shape analysis is based on an analysis framework of objects with spherical topology, described mainly by sampled spherical harmonics SPHARM-PDM. The input of the shape analysis framework is a set of binary segmentations of a single brain structure, such as the hippocampus or caudate. These segmentations are converted into a shape description (SPHARM) with correspondence and analyzed via Hotelling T^2 two sample metric. More... Zhao Z., Taylor W., Styner M., Steffens D., Krishnan R., Macfall J. , Hippocampus shape analysis and late-life depression. PLoS ONE. 2008 Mar 19;3(3):e1837. |

|
Particle Based Shape RegressionShape regression promises to be an important tool to study the relationship between anatomy and underlying clinical or biological parameters, such as age. We propose a new method to building shape models that incorporates regression analysis in the process of optimizing correspondences on a set of open surfaces. The method is applied to provide new results on clinical MRI data related to early development of the human head. M Datar, J Cates, P T Fletcher, S Gouttard, G Gerig, R Whitaker, Particle Based Shape Regression of Open Surfaces with Applications to Developmental Neuroimaging, MICCAI 2009. |
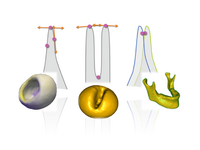
|
Geometric Correspondence for Nonregular SurfacesTo resolve the challenges posed by highly nonregular surfaces, we have proposed an efficient method which incorporates Geodesic distances and an entropy based on surface normals to improve correspondences. M Datar, Y Gur, B Paniagua, M Styner, R Whitaker,Geometric Correspondence for Ensembles of Nonregular Shapes, MICCAI 2011. |
|
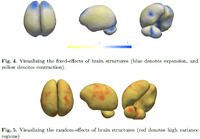
Mixed-Effects Shape Models for Longitudinal AnalysisLongitudinal shape changes in anatomy are characterized using a new method that combines point correspondences across shapes with the statistical modeling of individual and population trends via the linear mixed-effects model. This method helps us examine and contrast population trends with individual growth trajectories. New: M Datar, P Muralidharan, A Kumar, S Gouttard, J Piven, G Gerig, RT Whitaker, PT Fletcher,Mixed-Effects Shape Models for Estimating Longitudinal Changes in Anatomy, STIA 2012 |
|
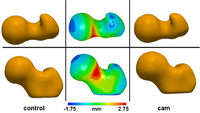
Statistical Shape Analysis of Cam-FAICam femoroacetabular impingement (FAI) is characterized by a malformed femoral head that may lead to early hip osteoarthritis. Radiographic measurements are used to diagnose cam FAI and often assume the femur shape to be spherical. Statistical shape modeling (SSM) can be used to compare complex 3D morphology without the need to assume ideal geometry and quantify morphologic differences between control and FAI femurs. New: MD Harris, M Datar, E Jurrus, CL Peters, RT Whitaker, AE Anderson, Shape Modeling of CAM-type Femoroacetabular Impingement, CMBBE 2012 |
|
Understanding Short Bone Phenotype in Multiple OsteochondromasNovel statistical methods were developed to study the 'steal phenomenon' caused by multiple osteochondromas in mouse models. Bone lengths and volumes were compared. Metaphyseal volume deviations from normal, as a measure of osteochondroma volumetric growth, were correlated with length deviations. New: KB Jones, M Datar, S Ravichandran, H Jin, E Jurrus, RT Whitaker, MR Capecchi, Toward an Understanding of the Short Bone Phenotype Associated with Multiple Osteochondromas, JOR 2012 (to appear) |
|
DTI Volumetric White Matter ConnectivityWe have developed a PDE-based approach to white matter connectivity from DTI that is founded on the principal of minimal paths through the tensor volume. Our method computes a volumetric representation of a white matter tract given two endpoint regions. We have also developed statistical methods for quantifying the full tensor data along these pathways, which should be useful in clinical studies using DT-MRI. More... |

|
DTI Processing and Statistics ToolsWe implement the diffusion weighted image (DWI) registration model from the paper of G.K.Rohde et al. Patient head motion and eddy currents distortion cause artifacts in maps of diffusion parameters computer from DWI. This model corrects these two distortions at the same time including brightness correction. |
|
Tissue Classification with Neighborhood StatisticsWe have implemented an MRI tissue classification algorithm based on unsupervised non-parametric density estimation of tissue intensity classes. More...
|
|
Atlas-Based Brain SegmentationWe have implemented an Multi-Atlases based brain MRI tissue segmentation method. This method using a fast,shape-based hierarchical matching approach to find the kNNs for a target brain in a brain dataset with known segmentations/labels, and then fuse the labels of the kNNs instead of the labels of all images in the dataset, which can give an accurate atlas for the target. P. Zhu, S.P. Awate, S. Gerber, R. Whitaker. Fast Shape-Based Nearest-Neighbor Search for Brain MRIs Using Hierarchical Feature Matching, MICCAI 2011. |